Click here to access page on tips and tricks in mathematics.
This online test is for general aptitute test and critical thinking. It deals with arithmetic, numbers, trigonometry, mensuration, coordinate geometry, puzzles, permutation and combinations. This test should be helpful in preparation and assessing one's progress for various recruitment tests such as banking and competitive examinations CAT, SAT.
Go to Home page.
Number of digits in products
Product of integers with N and M digits
N = 2, M = 3: 10 * 100 = 1000, D = 4 = [N + M - 1]
N = 2, M = 3: 99 * 100 = 9900, D = 4 = [N + M - 1]
N = 2, M = 3: 10 * 999 = 9990, D = 4 = [N + M - 1]
N = 2, M = 3: 99 * 999 = 98901, D = 5 = [N + M]
N = 2, M = 4: 10 * 1000 = 10000, D = 5 = [N + M - 1]
N = 2, M = 4: 99 * 1000 = 99000, D = 5 = [N + M - 1]
N = 2, M = 4: 10 * 9999 = 99990, D = 5 = [N + M - 1]
N = 2, M = 4: 99 * 9999 = 989901, D = 6 = [N + M]
Thus: the answer is N+M-1 and N+M.
Approximate Square Root of a number
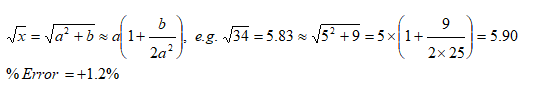
Last digit of power of 3, 4, 7 ...
Note:
3^4 = 81
3^5 = 243
3^6 = 729
3^7 = 2187
3^8 = 6561
Thus:
3^n = 1 if remainder(n/4) = 0
= 3 if remainder(n/4) = 1
= 9 if remainder(n/4) = 2
= 7 if remainder(n/4) = 3
Similarly, last digit of 4^n is 6 is n is an even number and 4 if n is an odd number.
Similarly, last digit of 7^n
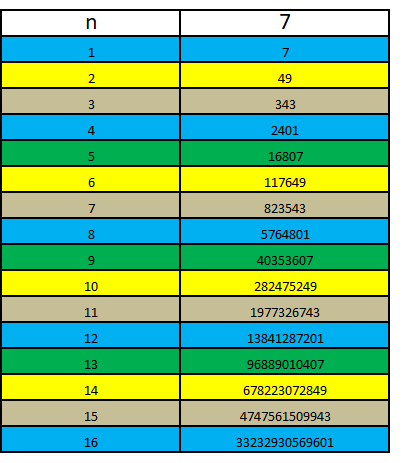
Thus:
7^n = 1 if remainder(n/4) = 0
= 7 if remainder(n/4) = 1
= 9 if remainder(n/4) = 2
= 3 if remainder(n/4) = 3