- Science and maths
Maths is Beautiful
Basic Mathematics for Everyone
Maths Tips and Trick incl. Vedic Mathematics
This page describes some of the key shortcuts in maths primarily in algebra such as multiplication, square, quadratic equations and large exponents of a number. Do you know that 2, 3, 7 and 8 cannot be at unit's place of a perfect square, that square of a number having 'n' digits will results in a number with 2n or 2n-1 digits, that the square of any odd number is sum to two consecutive numbers and so on. यह पृष्ठ गणित में मुख्य रूप से बीजगणित में कुछ प्रमुख संक्षिप्त रूप जैसे गुणन, वर्ग, द्विघात समीकरण और किसी संख्या के बड़े घातांक का वर्णन करता है। क्या आप जानते हैं कि 2, 3, 7 और 8 पूर्ण वर्ग की इकाई के स्थान पर नहीं हो सकते हैं, 'n' अंकों वाली संख्या के उस वर्ग का परिणाम 2n या 2n-1 अंकों वाली संख्या में होगा, जो कि किसी भी विषम संख्या का वर्ग होगा। संख्या दो क्रमागत संख्याओं का योग है और इसी प्रकार आगे भी।
That is: 52 = 12 + 13
92 = 40 + 41
...132 = 64 + 65
We have always been explained the standard method of finding the roots of a quadratic equation. Do you know that the first derivative of the equation = discriminant!
What is the time you will need to calculate 997×998? Using Vedic mathematics, you can simply write the product 997×998 = 995006!
वैदिक गणित में आकर्षक छिपे हुए रत्न शामिल हैं जो न केवल दिलचस्प हैं बल्कि गणना की गति को बेहतर बनाने में भी मदद करते हैं। यह एक पूरक पृष्ठ है जहां हम गणित में सलाह और चाल प्रदान करने का प्रयास करते हैं। मानक अभिक्षमता परीक्षणों से संबंधित प्रश्नों का वर्णन किया गया है जैसे कि विभाजनों में शेषफल खोजना, दक्षता विधि, कुल प्रयास विधि, गणितीय प्रवर्तनआदि। Vedic mathematics contain fascinating hidden gems which are not only interesting but also help improve calculation speed. This is a complementary page where we endeavour to provide tips and tricks in mathematics. The questions dealing with standard aptitude tests are described such as finding remainder in divisions, efficiency method, total effort method, mathematical induction and so on.
Division Rules
- Divisibility by 2: A number is divisible by 2 if digit at unit place is even.
- Divisibility by 3: A number is divisible by 3 if sum of all digits is also divisible by 3. E.g. 1323 is divisible by 3 because (1 + 3 + 2 + 3) = 9 which is divisible by 3.
- Divisibility by 4: A number is divisible by 4 if number comprising of digits at tens and units is divisible by 4. E.g. 123456 is divisible by 4 because 56 is divisible by 4.
- Divisibility by 5: A number is divisible by 5 if digit at unit place is either 0 or 5.
- Divisibility by 6: A number is divisible by 6 (2 x 3) if [a] digit at unit place is an even number - divisibility by 2 and [b] sum of all digits is divisible by 3 - divisibility by 3.
- Divisibility by 8: A number is divisible by 8 if number comprising of digits at hundreds, tens and units is divisible by 4. E.g. 123456 is divisible by 8 because 456 is divisible by 8.
- Divisibility by 9: A number is divisible by 9 if sum of all digits is also divisible by 9. E.g. 1323 is divisible by 9 because (1 + 3 + 2 + 3) = 9 which is divisible by 9.
The numerator is repeated, decimal place = number of digits less by 1. Example:
Step-1: 513/9 = 513 513 513 513 repeat the numerator.
Step-2: Location of decimal place = 2 (no of digits in 513) - 1. Thus, 513/9 = 51.3513 - Divisibility by 11: A number is divisible by the difference in sum of digits at alternate place is divisible by 11. E.g. 7238561 is divisible by 11 because [1+5+3+7] - [6+8+2] = 0 which is divisible by 11.
- [Reference: www.transum.org] Multiplication by 11 - bring down the last digits to unit's place, add the digit to the number on it's left and bring down the first number. Example: 15 × 11 [Step-1]Bring down 5 ➔ (15)(11) = --5, [Step-2]Add digit to left ➔ (15)(11) = -[1+5]5 [Step-3]Bring down the first number ➔ (15)(11) = (1)[1+5]5 = 165. 236 × 11 = 2[2+3][3+6]6 = 2596, 478 × 11 = [4+1][4+7+1=12][7+8=15]8 = 5258
- Divisibility by 12: A number is divisible by 12 (3 x 4) if [a] sum of all digits is also divisible by 3 and [b] number comprising of digits at tens and units is divisible by 4.
Puzzle for out of the box thinking: You need to move only 3 stars to change the orientation of pyramid upside down for given orientation: लीक से हटकर सोच के लिए पहेली: दिए गए अभिविन्यास के लिए पिरामिड के उन्मुखीकरण को उल्टा करने के लिए आपको केवल 3 सितारों को स्थानांतरित करने की आवश्यकता है:
*
* *
* * *
* * * *
New orientation:
* * * *
* * *
* *
*
Hint: Use the power of symmetry and you need to avoid any change to row 3. समरूपता की शक्ति का उपयोग करें और आपको पंक्ति 3 में किसी भी परिवर्तन से बचें।
गणित के सामान्य ज्ञान - Maths Trivia
(n+1)2 - (n+1) = n × (n+1). Thus: 72 - 7 = 42 = 6 × 7. 82 - 8 = 56 = 7 × 8.
642- 462 = (36-16)x100 - (36-16) = 1980. इस सूत्र के अनुसार विशेष परिस्थितियों में इतनी त्वरित गणना संभव है: Such quick calculations of special cases are possible as per the formula: (a.n+b)2 - (b.n+a)2 = (a2 - b2).n2 - (a2 - b2)
Do you find numbers 7, 11 and 13 boring? Not really, for any number abc x 7 x 11 x 13 = abcabc. For example, 369 x 7 x 11 x 13 = 369369. 963 x 7 x 11 x 13 = 963963.
If n is any digit between 1 and 9, nnn/3/n = 37. E.g. 666/18 = 777/21 = 37...
Multiplication by 9 - 9 से गुणा
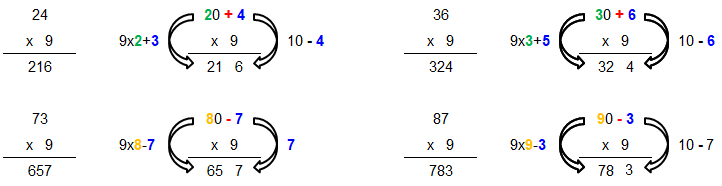
Multiplication by 11 - 11 से गुणा
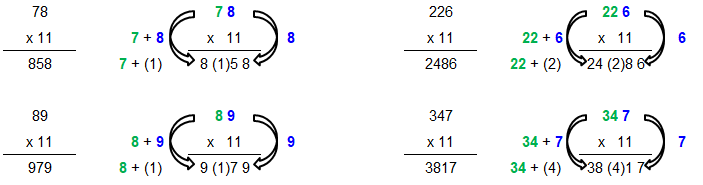
परिणाम में अंकों की संख्या - Number of digits in products
Product of integers with N and M digits
> N = 2, M = 3: 10 * 100 = 1000, D = 4 = [N + M - 1]N = 2, M = 3: 99 * 100 = 9900, D = 4 = [N + M - 1]
N = 2, M = 3: 10 * 999 = 9990, D = 4 = [N + M - 1]
N = 2, M = 3: 99 * 999 = 98901, D = 5 = [N + M]
N = 2, M = 4: 10 * 1000 = 10000, D = 5 = [N + M - 1]
N = 2, M = 4: 99 * 1000 = 99000, D = 5 = [N + M - 1]
N = 2, M = 4: 10 * 9999 = 99990, D = 5 = [N + M - 1]
N = 2, M = 4: 99 * 9999 = 989901, D = 6 = [N + M]
Thus: the answer is [N + M - 1] and [N + M].
Puzzle: Turn the fish by moving exactly 3 sticks
/ / \ / \ / \ \
संख्या का वर्ग - Square of a number
a2 = (a + b)*(a - b) + b2. For example: 43 * 43 = (43+3)*(43-3) + (3*3) = (46*40)+9 = 1849.
A great improvisation of this formula as per Vedic mathematics is as follows: "Whatever the extent of its deficiency, lessen it still further to that very extent; and also set-up the square of that deficiency". The calculations steps are then defined as:- Take the power of (10, 100, 1000 ...) nearest to the number being squared. E.g. n = 84 has base number b = 100.
- Calculate deficiency, d = b - n = 100 - 84 = 16
- Calculate square of the deficiency: d2. Write the right two digits, xx and carry the third digit if any say c. Here, d2 → 162 → xx = 56, c = 2
- Subtract twice of the deficiency from base and add the carry c. Thus: aa = b - 2 * d + c. Here: a = 100 - 2 * 16 + 2 = 70.
- Thus: 842 = aa|xx = 70|56 = 7056
- Note that this method is best suitable if the deficiency from suitable base (10, 100, 1000 ...) is in single digit. Some adaptation will be presented later.
- Followings are the specific applications of this rule:
- Square of any number ending is 5: eg. x52 = x*(x+1)|25. Thus: 752 = 7*8|25 = 5625, 1152 = 11*12|25 = 13225
- Square of numbers, when the sum of digits at unit's place is 10 and other digits are same, can be calculated using similar method. That is xy * xq where y + q = 10. xy * xq = x * (x+1)|p*q. For example: 67 * 63 = 6*(6+1)|7*3 = 4221.
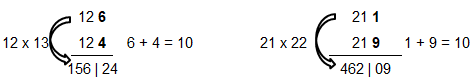
a2 - b2 = (a + b) × (a - b): This equation has many applications in solving maths problems quickly. इस समीकरण के गणित की समस्याओं को शीघ्रता से हल करने में कई अनुप्रयोग हैं For example:
- The sum of two numbers is 45 and their difference is 10. The difference of their squares = 45 × 10 = 450.
- The difference between the squares of two consecutive numbers is 25. Thus: a + b = 25 and a - b = 1 and hence a = 12, b = 13.
- The difference in squares of two consecutive number 50 and 51, that is 502 - 512 = (50 + 51) × (51 - 50) = 101.
- a2 + b2 = (a - b)2 + 2ab. Thus, if the product of two consecutive numbers is known, the sum of their squares = twice the product + 1.
- a2 + b2 = (a + b)2 - 2ab. Example, the sum of two numbers is 23 and their product is 126. Find the sum of squares of these numbers. a2 + b2= 232 - 2×126 = 277.
Trivia: the number of dots on dices are not put randomly. They are placed such that the numbers on opposite faces add up to '7'. पासों पर बिंदुओं की संख्या यादृच्छिक रूप से नहीं डाली जाती है। उन्हें इस तरह रखा जाता है कि विपरीत फलकों पर संख्याओं का योग '7' हो जाता है।
a3 - b3 = (a - b)3 +3ab(a - b): This equation has many applications in solving maths problems quickly. For example:
- दो क्रमागत संख्याओं के घनों के बीच का अंतर The difference between the cubes of two consecutive numbers = 3ab + 1. Thus, if the product of two consecutive number is 380, find the difference of their cubes. इस प्रकार, यदि दो क्रमागत संख्याओं का गुणनफल 380 है, तो उनके घनों का अंतर ज्ञात कीजिए। The answer would be 3×380+1 = 1141.
- The difference in cubes of two numbers is 14716 and difference between the two number is 4. Find the product of the numbers. a3 - b3 = 14716, a - b = 4, ab = [14716 - 43]/3/4 = 1221.
a4 - b4 = (a - b) (a + b) (a2 + b2): For two consecutive numbers: a2 + b2 = 2ab + 1, and hence a4 - b4 = (a + b) × (2ab + 1). Example: The sum of two consecutive numbers is 15 and their product is 56. Find the difference in their 4th exponent. a4 - b4 = 15 × (2×56 + 1) = 15 × 113 = 1695. Similarly, a4 + b4 = (a2 + b2)2 - 2a2b2: For two consecutive numbers: a2 + b2 = 2ab + 1, and hence a4 + b4 = (2ab + 1)2 - 2a2b2. Note that the sum of fourth exponent of any two consecutive number now can be evaluated from the product of these numbers.
Note: 24 raised to an even power always ends with 76, 24 raised to an odd power always ends with 24, 76 raised to any power ends with 76.
What is digit at unit's place of the number 792351681/5? The answer is 8. This is due to the fact that any number raised to its fifth power will have its last digit (that at unit's place) unchanged!
Puzzle with Numbers
Can you write a mathematical expression using 3 equal digits that results in value of 30? क्या आप 3 समान अंकों का उपयोग करके एक गणितीय व्यंजक लिख सकते हैं जिसके परिणामस्वरूप 30 का मान हो?Answer: 33 -3 = 30, 33 + 3 = 30, 6 × 6 - 6 = 30, 5 × 5 + 5 = 30. Same way similar questions can be framed such as 22 + 2 = 24, 44 - 4 = 40.
Can you write a mathematical expression using 3 equal digits that results in value of that digit itself? क्या आप 3 समान अंकों का उपयोग करके एक गणितीय व्यंजक लिख सकते हैं जिसके परिणामस्वरूप उस अंक का मान स्वयं वो अंक हो?Answer: Few trivial solutions are n + n - n = n or n × n / n = n or nth square root of nn. Only solution which is not trivial is 2 x 2 - 2 = 2.
Trick with Numbers
How quickly can you solve: 213 - 212? As it is difficult for most of the person to calculate 21 × 21 × 21 with first calculating 21 x 21, it is time consuming. If you note that (n+1)3 - (n+1)2 = n3 + 2n2+n, 213 - 212 = 203 + 2 × 202 + 20 = 8820.
Similarly, (n+1)3 - (2n+1)2 = n3 - n2 - n can be used to solve quickly without any complex multiplication, that is using only mental calculation of squares and cubes: 213 - 412 = 203 - 202 - 20 = 7580.
Yet another short-cut is (n+1)3 - (3n+1)2 = n3 - 6n2 - 3n can be used to solve 213 - 612 = 203 - 6 × 202 - 3 × 20 = 5540.
Another special case where the difference in cube of two consecutive numbers are to be calculated: (n+b)3 - (n+c)3 = [b-c] x [3n2 + 3n.(b+c) + (b-c)2 + 3bc]. Thus, if b-c = 1, (n+b)3 - (n+c)3 = 3n2 + 3n.(b+c) + 3bc + 1. Thus 733 - 723 = 3 x 4900 + 210 x 5 + 18 + 1 = 15769. If if b-c = 2, (n+b)3 - (n+c)3 = 2 x [3n2 + 3n.(b+c) + 3bc] + 23. If if b-c = 3, (n+b)3 - (n+c)3 = 3 x [3n2 + 3n.(b+c) + 3bc] + 33 and so on.
Large Exponent of a Large Number
10012 = 1002001. Hence, 10012 - 1 is divisible by 1000 or multiple of 1000 as per divisibility rules of 2, 3, 4 ...
10013 = 1003003001. Hence, 10013 - 1 is divisible by 1000 or multiple of 1000 as per divisibility rules of 2, 3, 4 ...
Special cases- 1111...12 [where '1' is repeated 'n' times] = 123..n(n-1)...1. e.g. 111112 = 123454321 where n = 5. This is valid till n ≤ 9.
For n ≥ 10: 111...1 2 = 12...79012..U..2098...1 where U = unit place of (n+1). For example, 1 repeated 12 times: 1111111111112 = 12345679012320987654321, here U = 3 in (12+1 = 13).
1 repeated 13 times: 11111111111112 = 1234567901234320987654321, here U = 4 in (13+1 = 14).
Exception: 1 repeated 10 times: 111111111112 = 1234567900987654321.
- 3333...32 [where '3' is repeated 'n' times] = 11..1088..89 where '1' and '8' are repeated 'n-1' times. e.g. 3333332 = 111110888889 where n = 6.
- 666...62 [where '6' is repeated 'n' times] = 44..4355..56 where '4' and '5' are repeated 'n-1' times. e.g. 66666662 = 44444435555556 where n = 7.
- 999...92 [where '9' is repeated 'n' times] = 99..9800..01 where '9' and '0' are repeated 'n-1' times. e.g. 99992 = 9999800001 where n = 4.
- Can you find a pattern in following square numbers formed by repetition of 2, 4, 5 and 8?

Trivia: Magic Square: A magic square is an arrangement of numbers in square shape consisting of the distinct positive integers N, N+1, N+2... (N = 1, 2, 3...) arranged such that the sum of the numbers in any horizontal, vertical or main diagonal line is always the same number. As the definition suggests, the number of rows and columns have to be equal. E.g.
4 9 2 3 5 7 8 1 64x4 square:
5 15 16 2 10 8 7 13 6 12 11 9 17 3 4 14
Approximate Square Root of a number - किसी संख्या का अनुमानित वर्गमूल
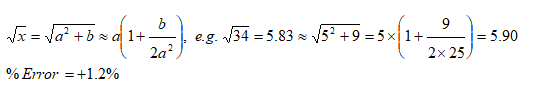
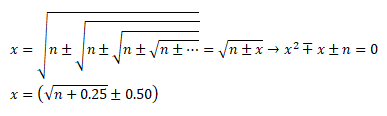
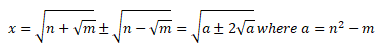
घात में अंतिम अंक (घातांक) - Last digit in power (exponent) of 3, 4, 7 ...
- 34 = 81, 35 = 243, 36 = 729, 37 = 2187, 38 = 6561
Thus:
3n = 1 if remainder(n/4) = 0
= 3 if remainder(n/4) = 1
= 9 if remainder(n/4) = 2
= 7 if remainder(n/4) = 3 - Similarly, last digit of 4n is 6 is n is an even number and 4 if n is an odd number.
- Last digit of 5n is always 5.
- Last digit of 6n is always 6.
- Last digit of 7n:
7n = 1 if remainder(n/4) = 0
= 7 if remainder(n/4) = 1
= 9 if remainder(n/4) = 2
= 3 if remainder(n/4) = 3
- 8n = 6 if remainder(n/4) = 0
= 8 if remainder(n/4) = 1
= 4 if remainder(n/4) = 2
= 2 if remainder(n/4) = 3
- Using the remainders described above, remainder of expressions like 334/5 can be easily obtained as explained below.
If Q = A × n + R, then remainder of Qm/n = remainder of Rm/n.
If Q = (A × n + R) and P = (B × n + S), then remainder of (Q * P)m/n = remainder of (R * S)/n.
Thus: remainder of 334/n = remainder[ { remainder of (34)8/5 × remainder(32/5) } / 5 ]
The trick is to break the larger exponent in smaller exponent such that remainder is 1.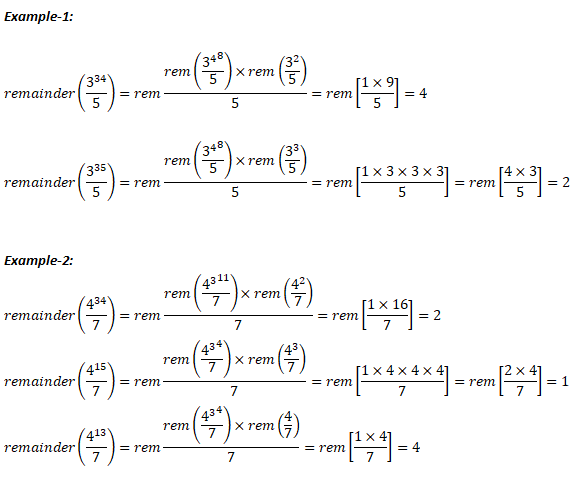
किसी संख्या के घन में इकाई के स्थान पर अंक में कोई परिवर्तन नहीं होगा यदि इकाई स्थान पर अंक 4, 6 या 9 हैं। इकाई के स्थान पर किसी अन्य अंक के मामले में, इसके घन में अंक होगा [10 - वह अंक ]. The cube of a number will have no change in digit at unit's place if the digits at the unit place are 4, 6 or 9. In case of any other digit at unit's place, the digit in its cube would be [10 - that digit]. E.g. 133 = 2197, 173 = 4913.
इसी प्रकार, किसी संख्या के वर्ग के वर्ग (किसी संख्या की चौथी शक्ति) में इकाई के स्थान पर या तो 1, 5 या 6 होता है। यानी यदि इकाई का स्थान एक विषम संख्या (5 को छोड़कर) है, तो उस संख्या का चौथा घातांक हमेशा 1 पर समाप्त होगा। इसी तरह, यदि इकाई का स्थान एक सम संख्या है, तो उस संख्या का चौथा घातांक हमेशा 6 में समाप्त होगा। Similarly, the square of square of a number (4th power of a number) has either 1, 5 or 6 at units place. That is if unit's place is an odd number (except 5), the 4th exponent of that number will always end in 1. Similarly, if unit's place is an even number, the 4th exponent of that number will always end in 6.
A combination of this the above rules can be used to find digit at unit's place for any other exponent (such as 6th, 8th, 10th ...) of a number. Use the following table to check the rules described thus far.| Number | X2 | X3 | X4 | X5 | X6 |
| 11 | 121 | 1331 | 14641 | 161051 | 1771561 |
| 12 | 144 | 1728 | 20736 | 248832 | 2985984 |
| 13 | 169 | 2197 | 28561 | 371293 | 4826809 |
| 14 | 196 | 2744 | 38416 | 537824 | 7529536 |
| 15 | 225 | 3375 | 50625 | 759375 | 11390625 |
| 16 | 256 | 4096 | 65536 | 1048576 | 16777216 |
| 17 | 289 | 4913 | 83521 | 1419857 | 24137569 |
| 18 | 324 | 5832 | 104976 | 1889568 | 34012224 |
| 19 | 361 | 6859 | 130321 | 2476099 | 47045881 |
Quiz Time: A tree grows such that its height doubles every fourth day. If its height was 50 [m] on sixty-fourth day, when was its height 25 [m]?
Cube root of exact cubes - सटीक घनों का घनमूल
| First digit of cube | First digit of cube root |
| 1 | 1 |
| 2 | 8 |
| 3 | 7 |
| 4 | 4 |
| 5 | 5 |
| 6 | 6 |
| 7 | 3 |
| 8 | 2 |
| 9 | 9 |
The number of digits in a cube root = number of 3 digit groups in original cube including a single digit or double digit group if there is any.
The first (leftmost) digit of the cube root can be guessed easily from the first group (leftmost) of the cube. Thus: 17,233,489,287: there are 4 groups of 3 digits. Hence, the cube root of this number will have 4 digits. The digit at unit's place, as per the table above will be 3. The digit at thousand's place will be 2 as 23 < 17. Alternatively, except 4, 6 and 9, the digit at unit place in = 10 - the digit.
Trivia: The following three consecutive numbers are the lowest that are divisible by cubes other than 1: 1375, 1376 and 1377 - (divisible by the cubes of 5, 2 and 3 respectively).
Simple Equations
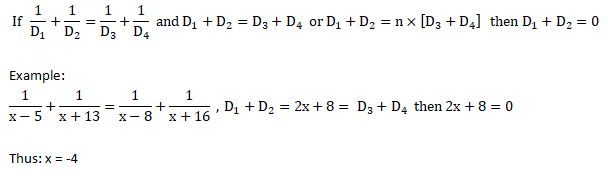
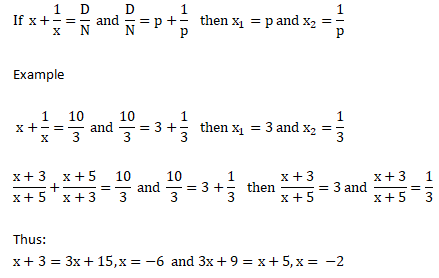
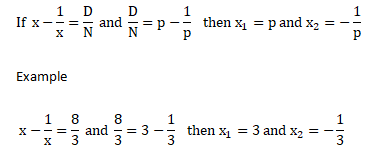
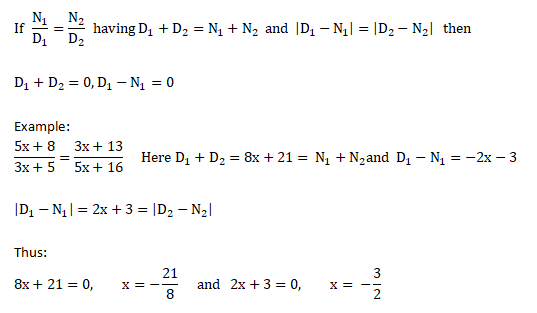
Find tens place of any exponent of a number ending in 1
E.g. tens place of 3157. The unit place would be 1. The tens place would be unit place of product (3 * 7) and hence 1 will be at tens place of 3157. The number is calculated at product of digit at tens place in the base that is '3' here and the first digit (at units place) in the exponent which is '7' here.
So far easy for exponents. How to find digit at ten's place in multiplication of 3 or 4 digits? Refer to the method below for product 24 × 37 × 68 × 94.
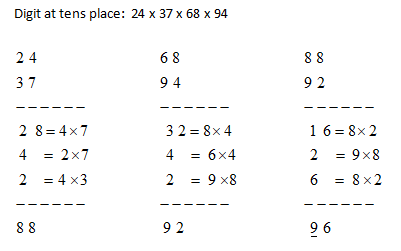
Work and time - Use efficiency as short-cut
If A does the task in 20 days and B does it in 16 days. How long will they take it to complete the task together?
Efficiency Method A's efficiency = 100/20 = 5%, B's efficiency = 100/16 = 6.25%, (A+B)'s efficiency = 5+6.25 = 11.25 %. Thus: Time required = 100/11.25 = 8.89 days
Another variant of such problem is given as:
If a group-A of 4 persons each of equal efficiency can do a task in 12 days. How many day would be required to do the same task by group-B of 6 persons with efficiency 2 times that of group-A?
Equality of total effort Let x be the efficiency of persons in group A. Total effort required = 4 * x * 12 = 48x [mandays]. This is constant for that particular task.
Now, let N be the number of days required for persons in group-B to complete the task. Thus: N * 2x * 6 = 48x. Hence, N = 4 days.
Sum of Arithmetic progression of numbers and squares - संख्याओं और वर्गों की अंकगणितीय प्रगति का योग
Arithmetic Progression
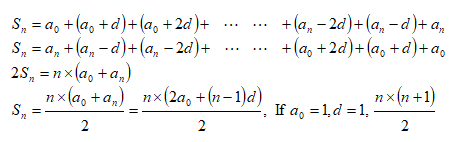
Sum of A.P. of squares
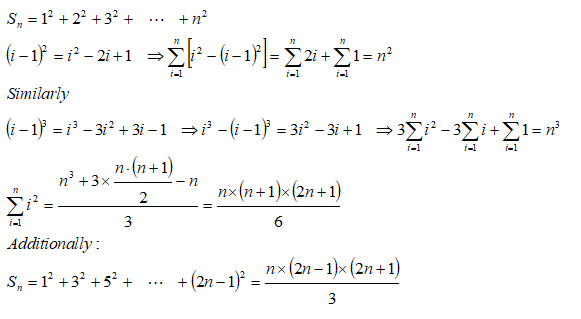
Sum of A.P. of Cubes and Products
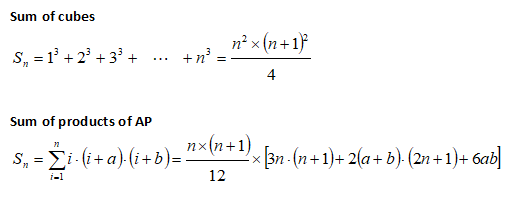
Sum of exponents of a number and its inverse
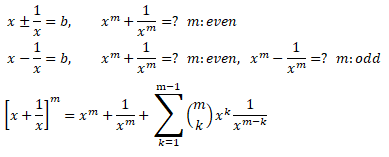
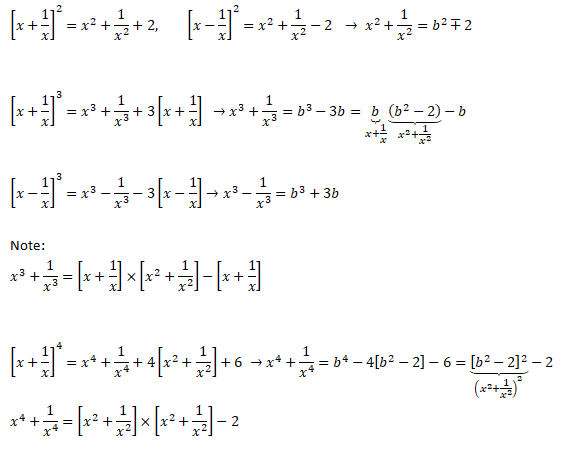
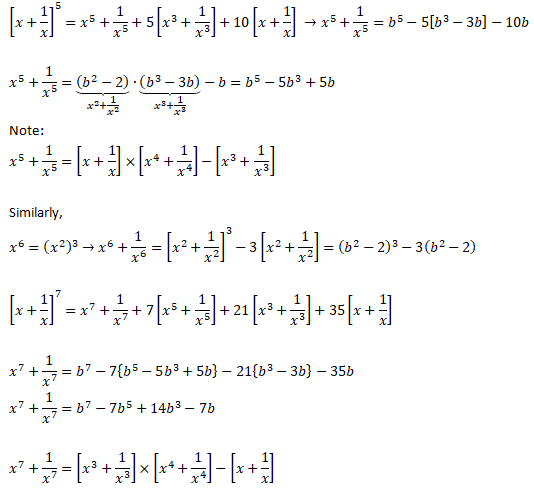
Vectors in Coordinate Geometry
Find length of BP, the projection of vector B over vector A.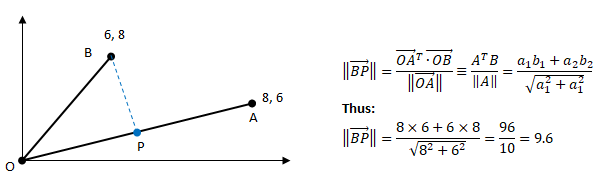
Quadratic Equations
The method to find roots of a quadratic equation is well known. However, there are times when the standard textbook method can be shortened. For example: a·x2 + b·x + c = 0 can be re-written asx2 + b/m · x + c/m = 0
If r1 and r2 are roots of the equation, (x - r1) × (x - r2) = x2 - (r1 + r2)x + r1×r2 = 0. Thus: r1 + r1 = -b/a and r1 × r2 = c/a.Example:
3·x2 + 2·x - 48 = 0, the shortcut is to find two numbers which adds to -2 and whose multiplication = -48. 6 and -8 are the numbers and hence the roots of the quadratic equation are [6/3, -8/3].Fractions: There are some general rules of the fractions which should be remembered to get answers quicker.
Puzzles
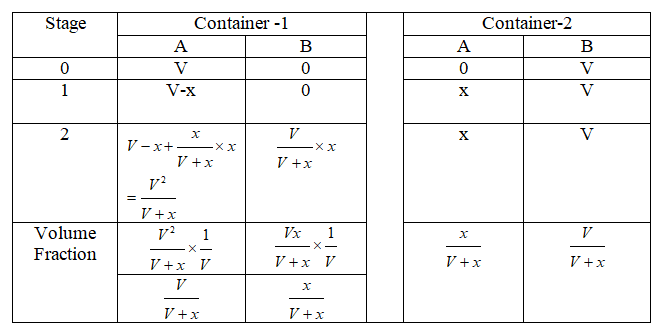
There are two containers having equal volume of A and B. Now, amount x of liquid A from container is taken out and mixed with liquid B. Thereafter, same volume x is taken out from second container and mixed with liquid A. Question is: which of the containers have higher impurity? In other words, is the volume fraction of B in A in the first container is higher, lower or same as volume fraction of A in B in the second container?
Answer: The volume fraction of B in A in container 1 = volume fraction of A in B in container 2. Before the answer is demonstrated through complex calculation, the easiest way to get to the answer is by noticing the variable 'x'. It can be between 0 to 100. Hence, assume the case when x = 100 and the answer is straightforward.
Trivia: Tower of Hanoi - Excertps from [mathworld.wolfram.com/TowerofHanoi.html] This puzzle was invented by E. Lucas in 1883. It is also known as the Tower of Brahma puzzle and appeared as an intelligence test for apes in the film Rise of the Planet of the Apes (2011) under the name "Lucas Tower".
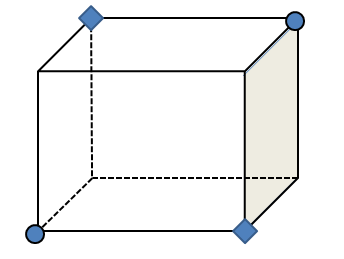
Puzzle: What is the shortest path between two diagonally opposite vertices of a cube when the travel path has to be all along the walls, ground and ceiling of the cube? Two such set of vertices have been shown by circles and diamonds in the following figure.
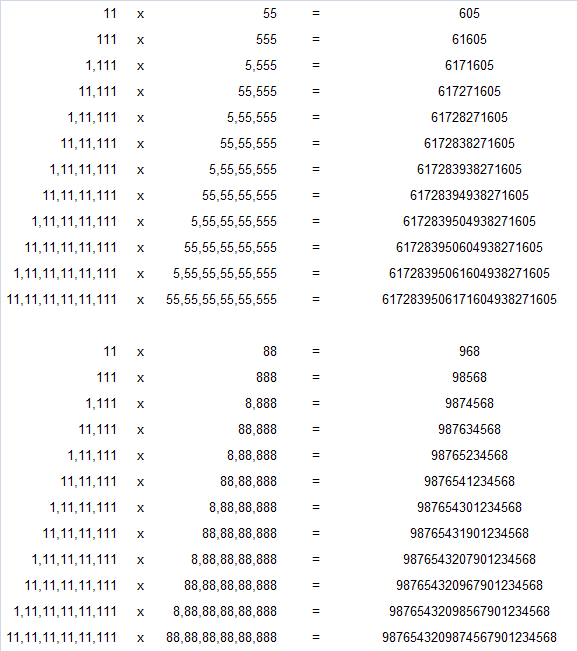
Multiplications of large numbers: can you find a pattern or data is insufficient?
More symmetry in maths
| 1 x 8 + 1 = 9 | 1 x 9 + 2 = 11 |
| 12 x 8 + 2 = 98 | 12 x 9 + 3 = 111 |
| 123 x 8 + 3 = 987 | 123 x 9 + 4 = 1111 |
| 1234 x 8 + 4 = 9876 | 1234 x 9 + 5 = 11111 |
| 12345 x 8 + 5 = 987 65 | 12345 x 9 + 6 = 111111 |
| 123456 x 8 + 6 = 987654 | 123456 x 9 + 7 = 1111111 |
| 1234567 x 8 + 7 = 9876543 | 1234567 x 9 + 8 = 11111111 |
| 12345678 x 8 + 8 = 98765432 | 12345678 x 9 + 9 = 111111111 |
| 123456789 x 8 + 9 = 987654321 | 123456789 x 9 +10 = 1111111111 |
| 1 x 1 = 1 | |
| 9 x 9 + 7 = 88 | 11 x 11 = 121 |
| 98 x 9 + 6 = 888 | 111 x 111 = 12321 |
| 987 x 9 + 5 = 8888 | 1111 x 1111 = 1234321 |
| 9876 x 9 + 4 = 88888 | 11111 x 11111 = 123454321 |
| 98765 x 9 + 3 = 888888 | 111111 x 111111 = 12345654321 |
| 987654 x 9 + 2 = 8888888 | 1111111 x 1111111 = 1234567654321 |
| 9876543 x 9 + 1 = 88888888 | 11111111 x 11111111 = 123456787654321 |
| 98765432 x 9 + 0 = 888888888 | 111111111 x 111111111 = 12345678987654321 |
Trivia
Kaprekar’s Constant - Take any four-digit number except an integral multiple of 1111 (i.e. don’t take one of the nine numbers with four identical digits). Rearrange the digits of your number to form the largest and smallest strings possible. That is, write down the largest permutation of the number, the smallest permutation (allowing initial zeros as digits), and subtract. Apply this same process to the difference just obtained. Within the total of seven steps, you always reach 6174. At that point, further iteration with 6174 is pointless: 7641–1467 = 6174. Example: Start with 8028. The largest permutation is 8820, the smallest is 0288, and the difference is 8532. Repeat with 8532 to calculate 8532–2358 = 6174. Your own example may take more steps, but you will always reach 6174.
- Other than the trivial examples of 0 and 1, the only natural numbers that equal the sum of the cubes of their digits are 153, 370, 371, and 407.
- Aside from 1, first positive number which is square and cube of a number is 64.
- 365 = 102 + 112 + 122 = 132 + 142
- 1 googol = 1100 - first used in 1940 by nine-year old Mitton Sirotta
- 1 + 4 + 6 + 7 = 18 = 2 + 3 + 5 + 8 and 12 + 42 + 62 + 72 = 102 = 23 + 52 + 82 + 12
- 1729 = 13 + 123 = 93 + 103- is known as Ramanujan-Hardy number. It is the smallest 'taxicab' number.
- Squares having odd number of divisors are called "perfect squares".
- Two consecutive prime numbers which differ by 2 are called Twin Primes.
- Interesting squares, exponents and summation from web:
- 71 + 73 + 71 + 77 + 77 + 73 + 78 = 13177388.
- 132 = 169, 312 = 961
- 206156734 = 26824404 + 153656394 + 187967604 - integer solution for the equation of the form x4 + y4 + z4 = a4 found by Noam Elkies.
- 2042 = 233 + 243 + 253
- 163 + 503 + 333 = 165033
- Lagrange’s Four Square Theorem: every natural number can be written as sum of squares of four non-negative integers (including 0) where numbers can be repeated. The summation for few Fibonacchi numbers are:
- 21 = 02 + 12 + 22 + 42 = 22 + 22 + 22 + 32
- 34 = 02 + 02 + 32 + 52 = 02 + 32 + 32 + 42 = 12 + 12 + 42 + 42 = 12 + 22 + 22 + 52
- 55 = 12 + 12 + 22 + 72 = 12 + 22 + 52 + 52 = 12 + 32 + 32 + 62
- 89 = 02 + 02 + 52 + 82 = 02 + 22 + 22 + 92 = 02 + 22 + 62 + 72 = 02 + 32 + 42 + 82 = 12 + 42 + 62 + 62
- Euler’s Equation: x3 + y3 + z3 = u3 No general solution exists though some specific solutions are expressed as following parametric form for arbitrary constants m and p.
- x = m7 - 3m4 (1+p) + m(2 + 6p + 3p2)
- y = 2m6 - 3m3(1+2p) + (1+3p+3p2)
- z = m6 - (1+3p+3p2)
- u = m4(m3-3p) + m(3p2-1)
- Exception: 13 + 63 + 83 = 93
- Another form of the parametric solution of Euler's equation is:
(6a2 - 4ab + 4b2)3 = (3a2 + 5ab - 5b2)3 + (4a2 - 4ab + 6b2)3 + (5a2 - 5ab - a2)3
- Yet another form of specific solution is given below when a2 + ab + b2 = 3mn2
(a+m2n)3 + (mb + n)3 = (ma + n)3 + (b + m2n)3
Integral of Trigonometric Squares
The following integration formula have wide applications in applications such as Fourier transforms, calculation of lift coefficient of airfoils...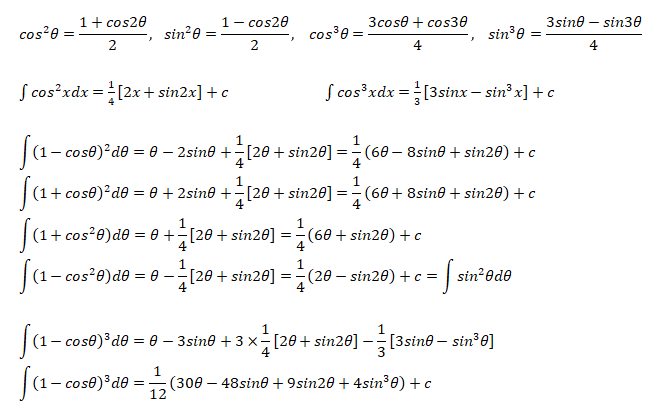
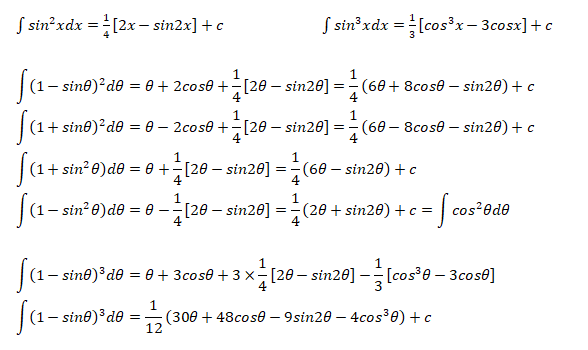
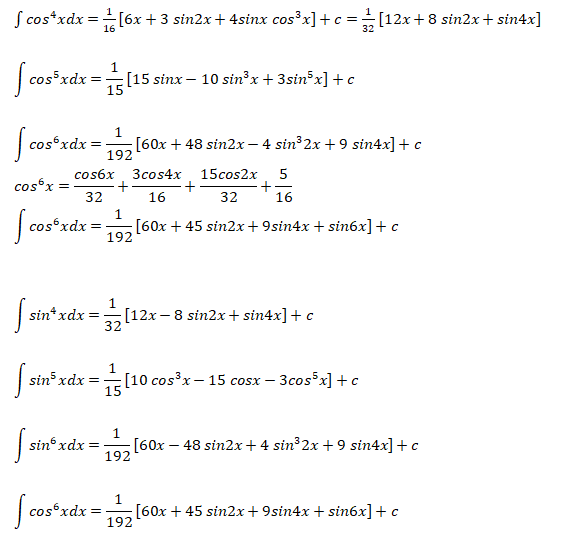
Multiply your Money
If you invest money which compounds annually:- (Approx.) number of years required to double the money = 72/ROI where ROI = annual rate of interest. E.g. if ROI = 4%, YTD (years to double) = 72/4 = 18 years. YTD varies as 70/ROI (ROI = 2%) to 75/ROI (ROI = 17%). Exact value = ln(2) / ln(1 + ROI/100).
- (Approx.) number of years required to triple the money = 115/ROI. E.g. if ROI = 4%, YTT (years to triple) = 115/4 = 24 years. YTT varies as 111/ROI (ROI = 2%) to 120/ROI (ROI = 19%). Exact value = ln(3) / ln(1 + ROI/100)
Lateral Thinking
This is an activity where children are encouraged to find a link between arrangement of words and numbers into standard phrases, something similar to clues given in a treasure hunt. Refer to few examples below: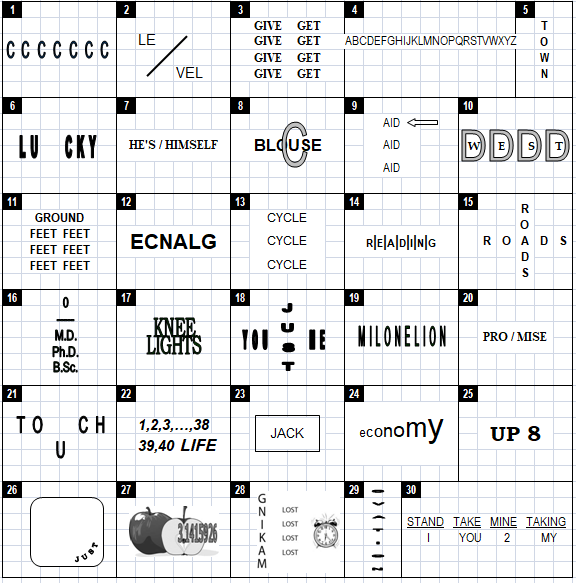
What is the next two letters in this sequence: B C D G J ... ...? The answers are: O and P. Why and how?
How many straight lines are required to connect 16 dots arranged in a 4 × 4 square, the lines must not cross each other?

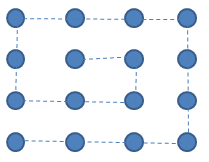
Move 3 sticks to show only 2 squares instead of 3 shown below.
O--------O--------O
| | |
| | |
O--------O--------O
| |
| |
O--------O
There are two ropes which takes total 1 hour to burn. These ropes may burn at different rates - but total time remains 1 hour. You have enough matchsticks to burn them as you need. How can you burn them to measure 45 minutes? Hint: Note that any special solution is part of a more generic solution!
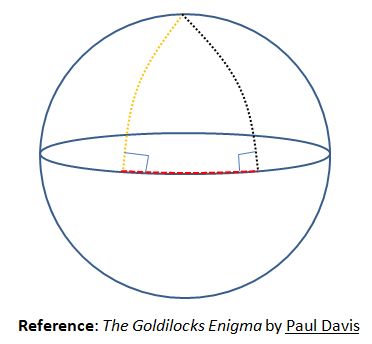
Can we have two right angles in a triangle? The classical textbook thinking will lead to answer in negative. That is because we always think triangles or rectangles to be formed by connecting ends of straight lines! What if the lines are not straight? Refer the image below and revisit your answer.
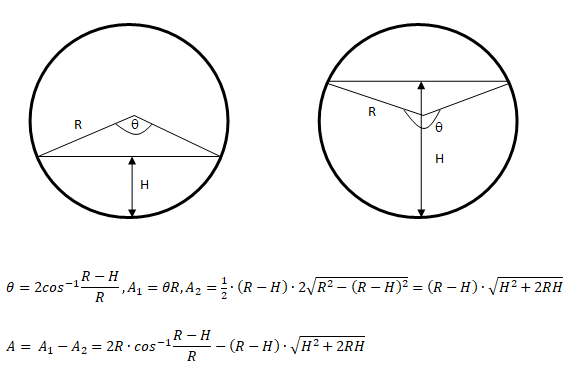
Area of a circular section cut by a chord
Integration: exponential-harmonic function
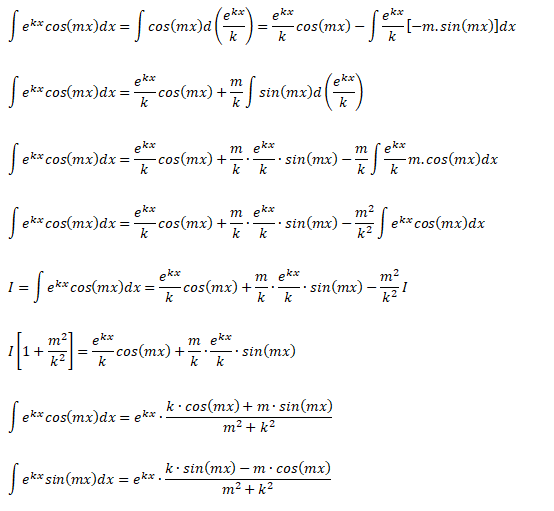
The content on CFDyna.com is being constantly refined and improvised with on-the-job experience, testing, and training. Examples might be simplified to improve insight into the physics and basic understanding. Linked pages, articles, references, and examples are constantly reviewed to reduce errors, but we cannot warrant full correctness of all content.
Template by OS Templates