Octave Script

Transient Conduction

OCTAVE is a free program highly compatible to MATLAB. It is a handy tool to solve differential equations numerically with built-in feature or use numerical methods dealing with inversion of matrices. A graphical plot of the results can be generated with ease.

The purpose of this calculation approach is to demonstrate the numerical technique and TDMA (Tri-Diagomal Matrix Algorithm) method to solve transient conduction. Various improvisation is possible in this script such as implementation of Heat Flux and Convective boundaries at the tip, incorporating variable cross-section area such as tapered rod and so on.

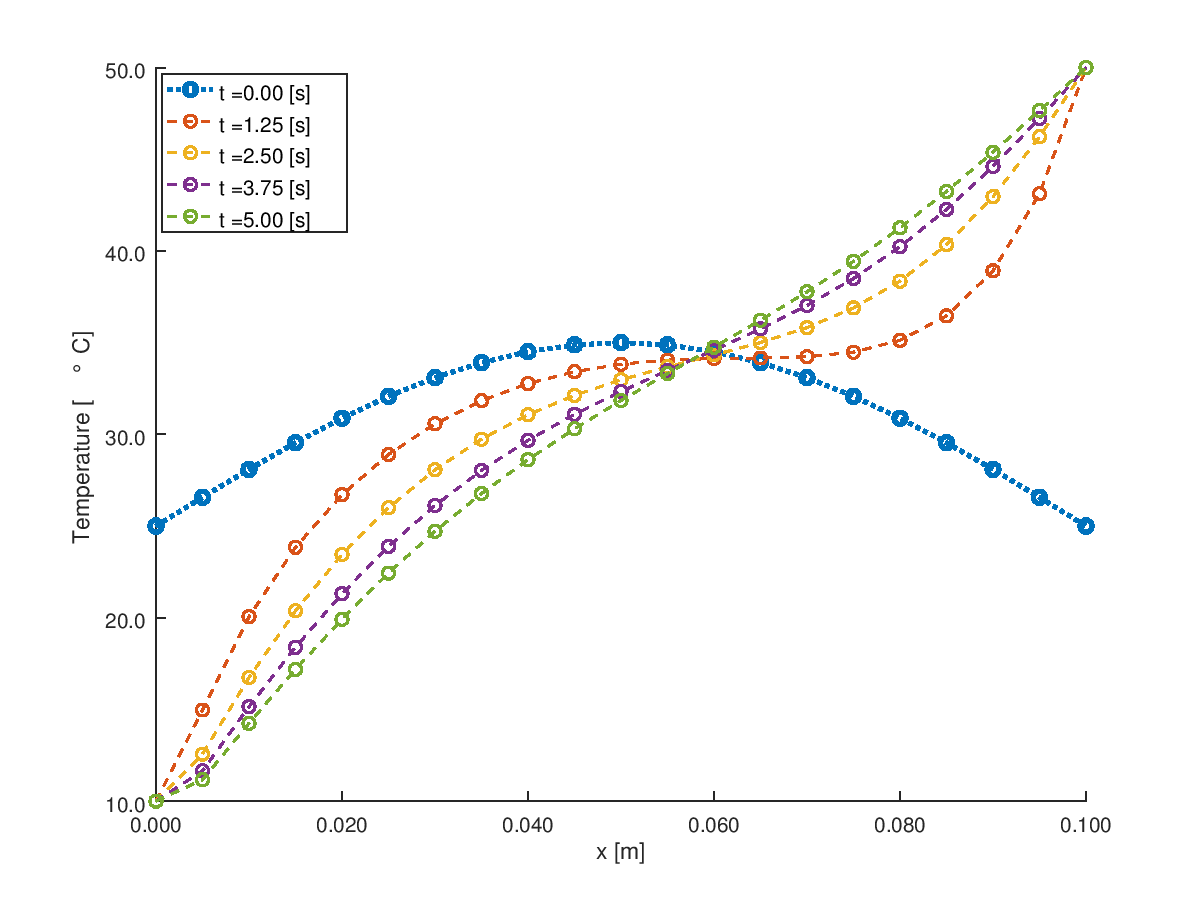
Temperature Time History Plots

% Solve 1D heat equation with Backward Time Centre Space scheme
%   d^2T     1      dT
%   ---- = ----- * ----
%   dx^2   alpha    dt
%
  clear; clc;

% L        = length of the domain [m]
  L        = 0.1;
% NN       = number of mesh nodes [number]
  NN       = 21;

% nTime    = number of steps  [number], delta_t = tMax / nTime
  nTime    = 4;
% tMax     = maximum time for the simulation [s]
  tMax     = 5.0;

% alpha    = diffusion coefficient [m^2/s]
% Thermal conductivity [W/m.K] 
  k        = 150;
% Density [kg/m^3]
  rho      = 2700;
% Specific heat capacity [J/kg.K]
  Cp       = 450;
  alpha    = k/rho/Cp;
  
% Specify initial conditions
  dx  = L / (NN - 1);
  x   = [0 : dx: L];
  phi = 25 + 10 * sin(pi .* x / L);
% Specify boundary conditions
  phi0     = 10; 
  phiL     = 50;
  
  dt = tMax / nTime;
  
% Check for Courant number for numerical stability and bounded solution
  CoNum = alpha * dt / dx^2;
  %If (CoNum >= 2.0) 
  %  N = L / ((alpha * dt / 2.0)^0.5);
  %	 NN = round(N);
  %  dx = L / (NN - 1);
  %endif
  
% --- Coefficients of the Tri-Diagonal System

% T^n(i-1) - 2T^n(i) + T^n(i+1)     1      T^n - T^[n-1](i)
% ----------------------------- = ----- *  --------------
%             dx^2                alpha         dt
%                     .--              --.
%   alpha             |  1     2*alpha   |          alpha            T^[n-1](i)
% - ----- T^n(i-1) +  | --- -  -------   |T^n(i) -  -----T^n(i+1) =  ----------
%    dx^2             |  dt     dx^2     |           dx^2                dt
%                     |__              __|
%
% -  C * T^n(i-1) +         A *          T^n(i) - B *   T^n(i+1) = d(i),  i = 1 ... NN 
%     
%  A* T^n(i) = B(i) * T(i+1) + C(i) * T(i-1) + d(i), i = 1 ... NN 

% subdiagonal C: coefficients of phi(i-1)
  B = (alpha/dx^2) * ones(NN,1);
  
% superdiagonal B: coefficients of phi(i+1)
  C = B;
  
% diagonal A: coefficients of phi(i)
  A = (1/dt) * ones(NN, 1) + 2 * B;

% constant term d
  d = zeros(NN, 1);
  
% Plot temperature profile at t = 0 [s]
  hold on; 
  plot(x, phi, "linestyle", ":", "linewidth", 2, "marker", "o");

  for m = 1:nTime
    % Tridiagonal Matrix Algorithm [Ref: S. V. Patankar]
    % If T(1) is specified
	A(1) = 1;     B(1) = 0; 
	
	% Since T(0) and T(NN+1) have no significance
	B(end) = 0;     C(1) = 0;
	
	d(1) = phi0 / dt;
	
	P(1) = B(1) / A(1);
    Q(1) = d(1) / A(1);
    for i = 2: NN
      d(i) = phi(i) / dt;
	  P(i) = B(i) / (A(i) - C(i) * P(i-1));
      Q(i) = (d(i) + C(i) * Q(i-1)) / (A(i) - C(i) * P(i-1));
    end
	phi(NN) = phiL;
	
    % --- Backward substitution 
    for i = NN-1 : -1 : 2
      phi(i) = P(i) * phi(i+1) + Q(i);
    end
	phi(1) = phi0;
	
    plot(x, phi, "linestyle", "--", "linewidth", 1, "marker", "o");
  end
  
  xlabel('x [m]');  	ylabel('Temperature [\deg C]');
  %grid on; set (gca, "ygrid", "on");

% Format X-axis ticks
  xtick = get (gca, "xtick"); 
  xticklabel = strsplit (sprintf ("%.3f\n", xtick), "\n", true);
  set (gca, "xticklabel", xticklabel)   
	
% Format Y-Axis ticks
  ytick = get (gca, "ytick"); 
  yticklabel = strsplit (sprintf ("%.1f\n", ytick), "\n", true); 
  set (gca, "yticklabel", yticklabel);
	
  legengTxt = cell(nTime+1, 1);
  for m = 0: nTime	
    legendTxt{m+1} = strcat('t = ', num2str(m * dt, '%.2f'), ' [s]');  
  end
  legend(legendTxt, "location", 'northwest');
  hold off; 
  print -dpng transCondOneD.png -color -landscape;