Probabilistic Numerical Method

Monte Carlo Simulation

Monte Carlo method is a probabilistic numerical method applied to a variety of mathematical problems based on (computer assisted generation of) random numbers.
  There are many numerical methods to solve steady as well as unsteady heat conduction problems. Monte Carlo method is unique in the sense that it is based on probability which is analogous to movement of atoms in a solid when heated. In sort, Monte Carlo method can be applied to most diffusion controlled process. However, there are few constraints on this method as well - the method in its basic form can be applied only on uniform grids and regular straight edge geometries. However, this restriction is not per say of the Monte Carlo method but the way nodes are created and boundaries are defined. For example, this method can also be applied to a circular plate if the 4 boundaries are 4 quarter arcs of the circumference of the plate and uniform element size are maintained. The uniform element size has to be enforced to comply with assumption of equal probability of random movements in all 4 directions.
  Few other examples include - Direct simulation Monte Carlo (DSMC) method which is a Monte Carlo style of simulation applied to dilute gas flows on molecular level as much as DSMC is the basic numerical method in the kinetic theory of gases and rarefied gas dynamics as on date.

Finite Difference Method vs. Monte Carlo Simulation

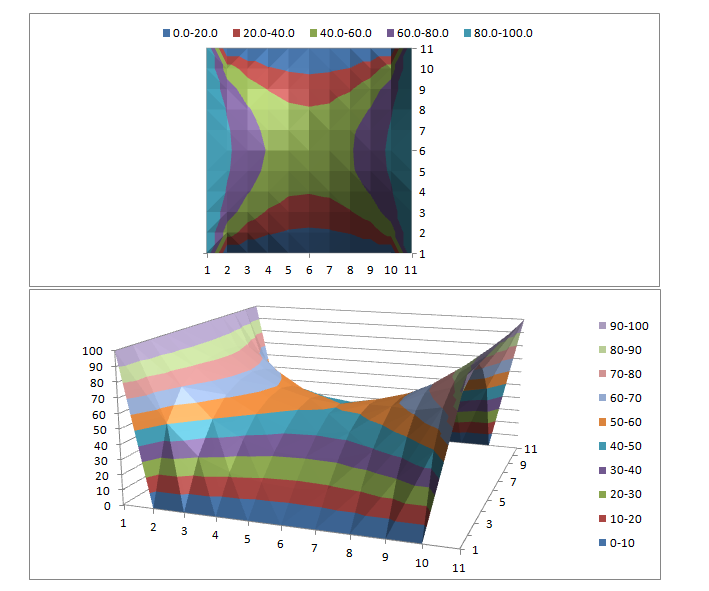
Typical result plots in Excel

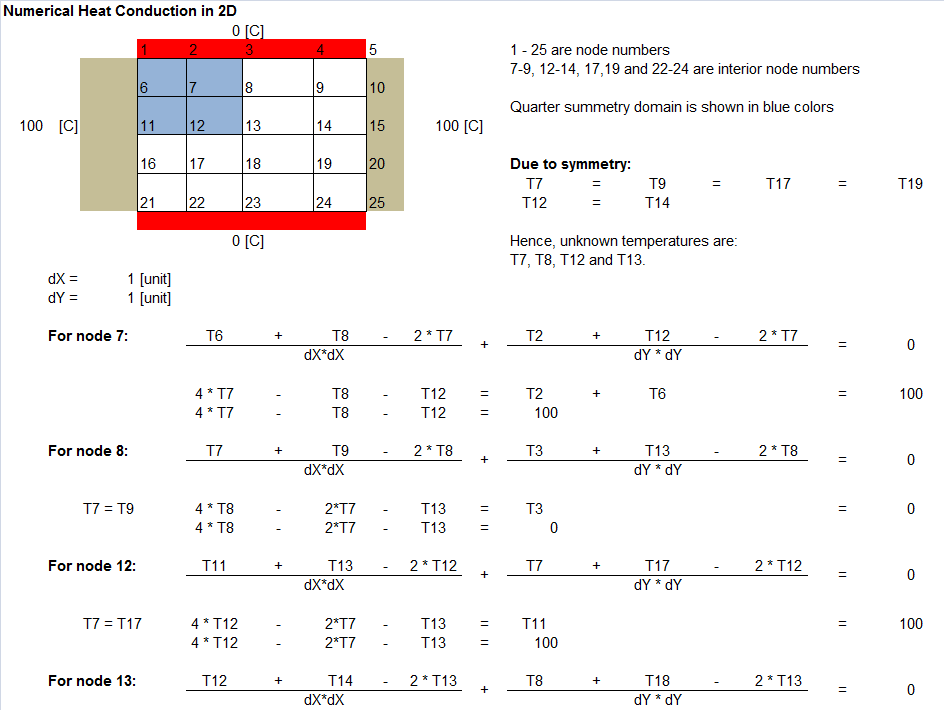
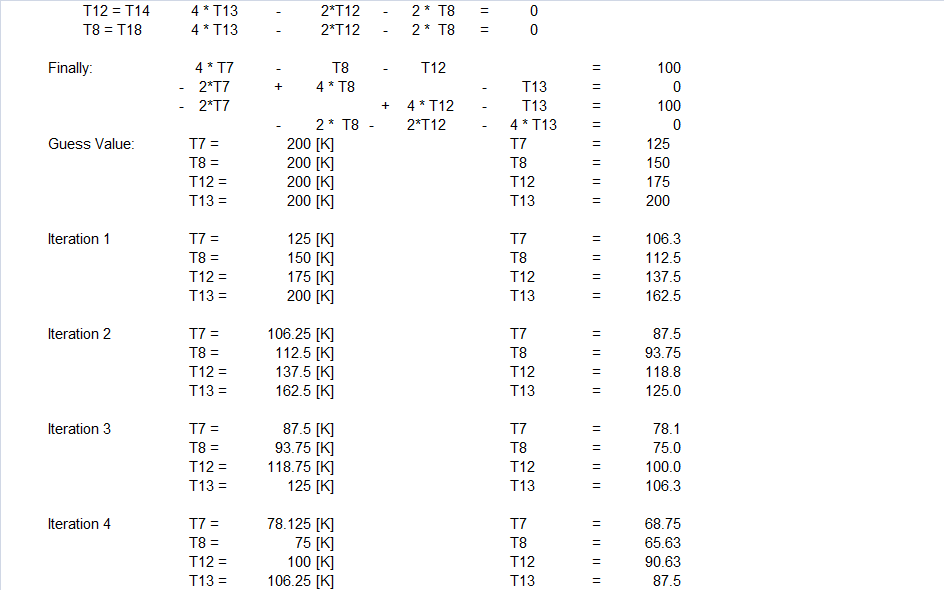
Same problem when solved using Finite Difference Method