Solid Mechanics: Formula and examples

Navier-Stokes Equation for Solid Deformation

Analogy between Solid Deformation and Fluid Flow

Example solutions in solid mechanics and strength of material, equivalence of Structural and Fluid Mechanics: At the fundamental level, the governing equations of fluid mechanics ("relatively LARGER" deformation and kinematics of fluids particles) and structural mechanics ("relatively SMALLER") deformation and kinematics of solid particles) are equivalent.

Navier-Stokes Equation for Solid Mechanics

Stress-strain formula

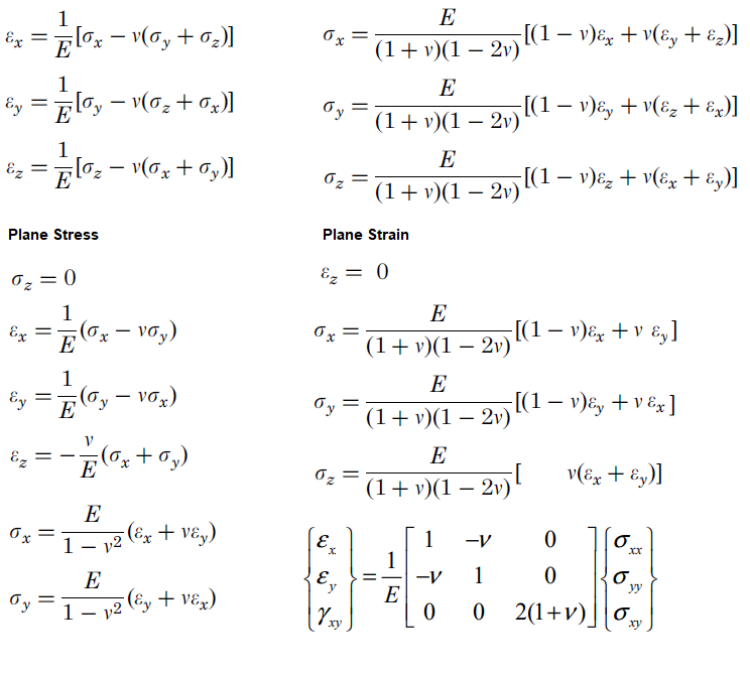
Stress-strain formula in algebraic form

Stress-strain formula in matrix form

Deflection of Beams

The layout of a general beam with varying cross-section is shown below.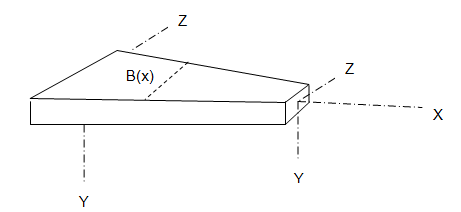

Beam Deflection Schematic

Differential equation of deflection curve:

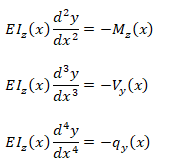
Beam Deflection Equation

Deflection by Area-Moment Method: distance of point B on a beam from tangent at point A on the beam is equal to the moment with respect to the vertical through B of the area of the bending moment diagram between A and B divided by flexural rigidity EI_Z.

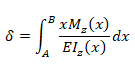
Beam Area Moment

Bending of a trapezoidal plate or tapered beam subject to uniform pressure 'p':

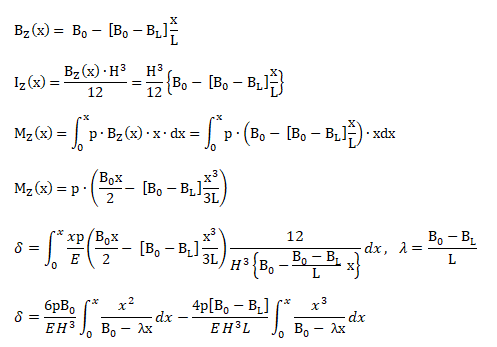
Tapered Beam Bending

No analytical expression exists for these integrals. However, it can be integrated analytically if the tapered beam ends at zero widths (sharp edge) and is shifted to the tip instead of the base. In this case, B_Z(x) = B_L × (x/L).

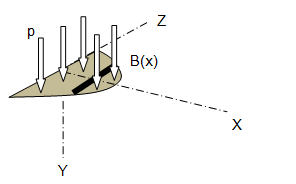
For bending of circular disk supported at one of its diameter and under uniform pressure 'p', H = thickness of the plate and symmetric half is shown below:

Circular Plate Layout

The deflection at any location x is given by:

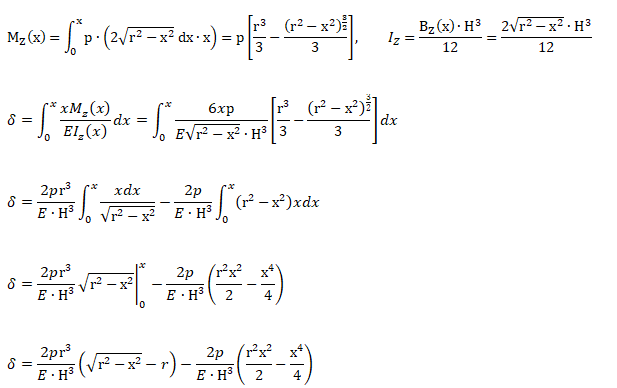
Circular Plate Bending Equation

Bolted Joints

Pre-load = tension in bolt (due to tightening) as net elongation of bolt which is difference of change in length of the bolt and compression of the clamped member.
Service Load = external force acting on the clamped member.
Bolted-joint Diagram: this is a "external force" vs. "bolt elongation" curve used to describe variation in clamping force with respect to applied force.

Mulitplication of Matrices

The mutliplication of matrices requires at least two loops and it becomes a bit complicated to chose the correct counter of indices to the arrays storing these matrices.

Multiplication of Matrices index Notation

The for loop to implement the steps and index notation defined above is as follows.

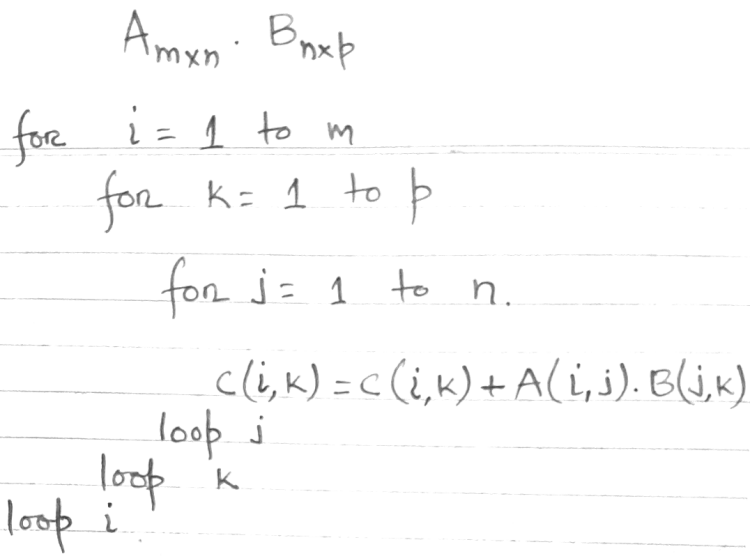
Multiplication of Matrices For Loops

The same operation using transpose of a matrix can be implemented in a bit different manner as shown below.

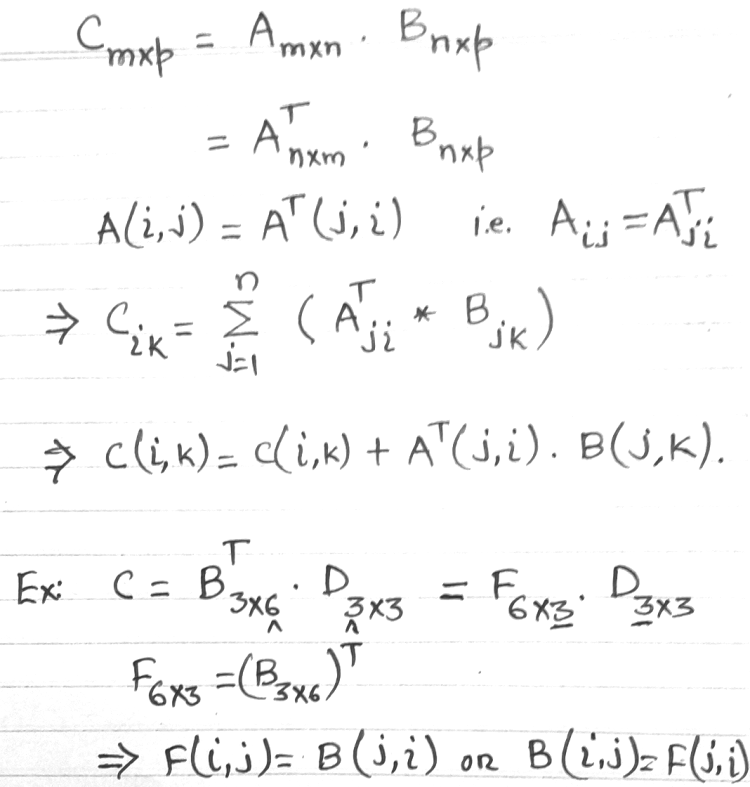
Multiplication of Matrices Step-3

The content on CFDyna.com is being constantly refined and improvised with on-the-job experience, testing, and training. Examples might be simplified to improve insight into the physics and basic understanding. Linked pages, articles, references, and examples are constantly reviewed to reduce errors, but we cannot warrant full correctness of all content.

Template by OS Templates