- CFD, Fluid Flow, FEA, Heat/Mass Transfer
- ***
- fb@cfdyna.com
College Physics
Text-book Solutions
Physics at College and Pre-Engineering Level
This page contains summary of formula in college physics, step-by-step solutions to problems in statics, dynamics, vibrations, simple harmonic motion. The basic concepts of physics such as FBD (Free-Body-Diagram) has relevance throughout the engineering course as well as design solutions to industrial needs. The Newton's law of motion, energy-mass-momentum conservation, work energy theorem are the basic building blocks to address any problem in mechanics. Please note that some prior knowledge of kinematics, mechanics and statics at college level is required.
To start with, note the following critical points
- While drawing a free-body-diagram (FBD) of any particle or system: always draw the force applied ON the particle and not forces applied BY the particle.
- Most of the time, questions in mechanics deal with vectors and hence direction is important. Always draw your own 'positive' and 'negative' directions and write vector consistent with chosen directions.
- You may frequently encounter situations where you need to find angle between direction of gravity and an inclined plane. Remeber the rule: "Angle between two lines = angle between lines perpendicular to those lines".
- Double check that the every step of calculation is dimensionally correct. Else, must check the dimensional consistency of final result.
- A body which is simultaneously rotating and translating will have two components of kinetic energy.
- Sometimes, a problem can be solved using "principle of conservation of total energy" in addition to method using Newton's law of motion. The former approach tends to be easier and less prone to error.
- Centripetal force on a rotating body is the effect of rotation and not the cause of rotation. Hence, the net force acting on a rotating body after accounting for gravity, tension in the rope to which it is attached... should be equal to the centripetal force mv2/r where m, v and r represent mass, velocity and radius.
- The principle of the conservation of momentum can be used ONLY for systems not acted upon by EXTERNAL FORCE(s).This is most useful when it can be recognized that by treating several bodies together as a system where the unknown forces will occur as equal and opposite pairs and will thus cancel out. Refer to an example below.
- Apply the "equilibrium of forces or Newton's second law of motion" and "conservation laws" on 'systems' and 'particles' separately and consistently. Sometimes it is convenient to consider a group of particles as system. For example, refer to the following case where there is totally inelastic collision between a ball and a vertical rod. Consider the following two cases.
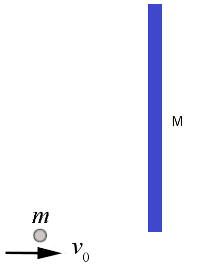
- If the ball and the rod are consider separate systems:
- The conservation of linear momentum still holds true between ball and rod.
- The angular momentum of rod before collision is zero. Hence, its angular momentum after collision about point of collision is zero (since any force due to collision acts at this point and hence there is no torque).
- One needs to chose an appropriate point on the rod to calculate angular momentum which gets trickier because final velocity of the "ball-rod" system will also contribute.
- This approach certainly looks complicated. Compare with the simplicity outlined below.
- If the ball and the rod are consider as single system:
- The conservation of linear momentum still holds true between ball and rod but with respect to the centre of mass of the system. The linear momentum before collision is only due to the ball and linear momentum after collision is due to common velocity of the centre of mass of the "ball-rod" system.
- There are no external torques acting on this system so the angular momentum about the center of mass of the ball-rod system is constant before and after the collision.
- The problem simplifies to calculating the centre of mass of the system.
- The angular momentum before collision needs to be calculated due to velocity of the ball about the centre of mass of the system. The angular momentum after collision and mass moment of inertia also need to be calculated about the centre of mass of the system.
- If the ball and the rod are consider separate systems:
- Change in the potential energy of the force when it causes displacement from point A to point B, (UB - UA) = negative of the work done by the force as it moves from A to B. Thus, the work done by the particle on which the force act, W = (UB - UA). Here, U is potential energy (not velocity).
- Equivalent values of springs and capacitors are calculated in similar fashion when connected in series (as harmonic sum) and parallel (arithmetic sum).
- Equivalent values of (electrical and thermal) resistances and electrical inductances add in similar fashion when connected in series (as arithmetic sum) and parallel (harmonic sum).
- 'Specific' value of any variable is per unit mass of that variable. For example, density is specific volume that it volume occupied by unit mass say 1 [kg]. Specific energy is energy per unit mass and its unit is [J/kg].
- 'Flux' value of any variable is per unit area of that variable. For example, intensity of light is energy passing though unit area say 1 [m2] and its unit is [J/s/m2]. Similarly, mass flux is flow of mass per unit area and its unit is [kg/s/m2], velocity is flow of volume per unit area and its unit is [m3/s/m2] = [m/s]. Electric field intensity is a special case which is defined at a point.
Summary of Physics Formula


The principle of the conservation of momentum can be used only for systems not acted upon by external forces. This principle is most useful when it can be recognized that by treating several bodies together as a system certain unknown forces will occur as equal and opposite pairs and will thus cancel.
Conservation of Mechanical Energy
The principle of the conservation of energy is applicable only to systems for which a potential energy can be defined. The work-energy equation (derived earlier) is more general than the equation of conservation of energy. This is so because work-energy equation applies to non-conservative systems (such as systems with frictional losses) as well as conservative systems.Collision
Direct central impact refers to collision situation when "direction of rebound" is same as "direction of approach". The velocities after impact in case of perfectly elastic collision is: 
- The motion of the center of mass is the same as the motion of a particle, having a mass equal to the total mass of the system, acted upon by the resultant external force. Though, the line of action of the resultant force may or may not pass through the centre of mass.
- Similarly, total work done by all of gravity forces acting on a system is given by the product of the total weight and the vertical distance moved by the center of gravity.
- As described above, the force of gravity varies inversely as the square of the distance from the centre of the Earth. An object say satellite or a projectile in space is thus acted upon by gravitational force FGRAV = - W * R2 / r2, where W is the weight of the particle or object at the Earth's surface, R is the radius of the earth and r is the radial position of the object from centre of the Earth.
- Analogy between gravitational and electrical potential: The potential of a spherical shell at any point outside the shell is G*m/r. Thus, the potential of a spherical shell at any point inside the shell is constant, and hence the gravitational attraction force on a mass inside a shell is zero.
- Based on previous conclusion, the gravitational attractive force between a point mass m and a uniformly distributed mass M of a sphere having radius R, FOUT = G * M * m / r2, when m is outside M that is r > R. The force is FIN = G * M * m * r / R3, when m is inside of the sphere.
Video with explanation of concepts of Analogy, Superposition and Symmetry
Calculations on Projectile
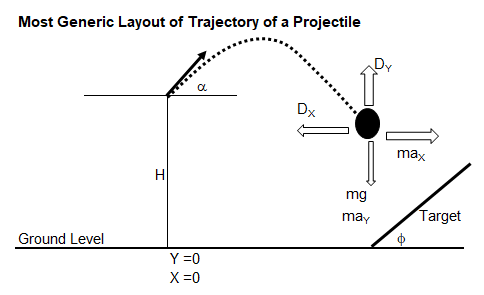
When air drag is negligible and there is no inclined target, that is projectile finally hits the ground.
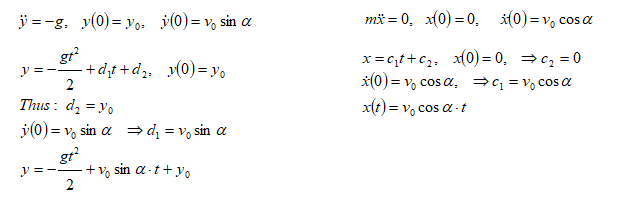
When projectile hits the ground, y = 0. Thus, the axial travel of projectile can be calculated as:
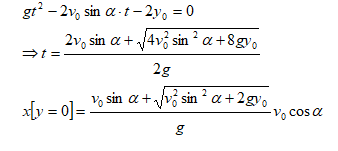
When projectile is launched from ground level, y0 = 0
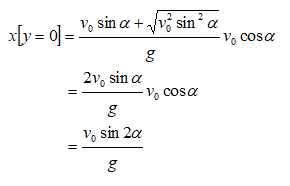
Conditions for Collision of Two Projectiles
Now let’s analyze situations when two projectiles are launched with a time gap. The conditions of two projectiles to collide with each other will be investigated. Now, the necessary and sufficient condition is that the two projectiles are at same coordinates (x, y) at later instant of time to collide. Thus: Equating the x-locations:
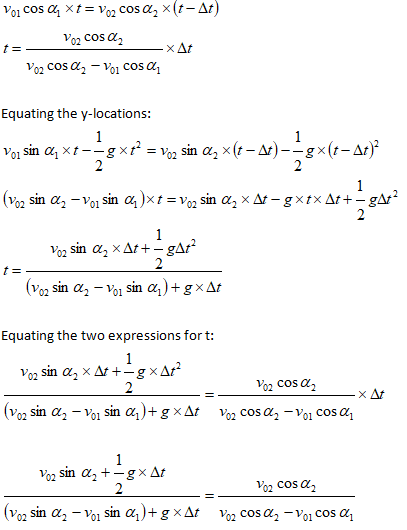
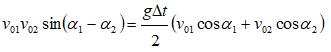
Inelastic Collision and Spring Compression
Collision is based on conservation of momentum and loss of energy defined by coefficient of restitution. This solution describes a case where one of the colliding objects is attached to a spring.

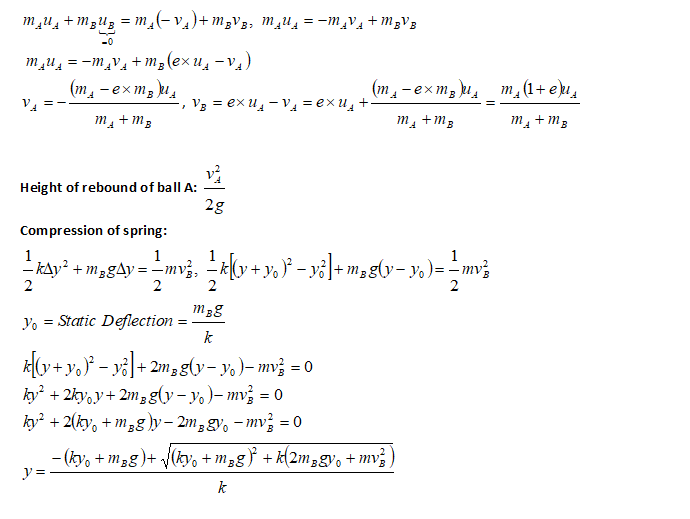
A rod of mass 'M1' and length 'L' is rotating on a frictionless horizontal surface at angular speed ω about its mid point. A point mass 'm2' moving at speed 'V' collides at radius 'R' in a tangential direction (perpendicular to the rod) opposite to rotation of the rod and sticks to it. For what value of 'R' the rotating rod will stop rotating instantaneously after collision? Detailed explanation on solving problems related to Inelastic Collisions is described in this PDF file and animation below.
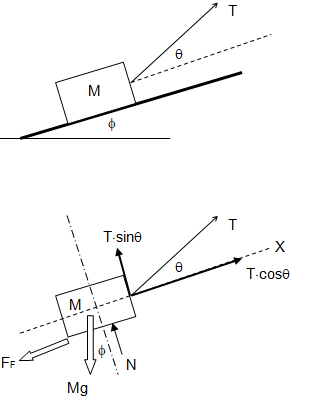
Block Sliding down an Inclined Plane
Find the acceleration and tension in the cord. The cord is assumed to be inextensible.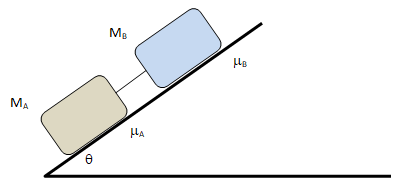
The free-body-diagram is shown below.
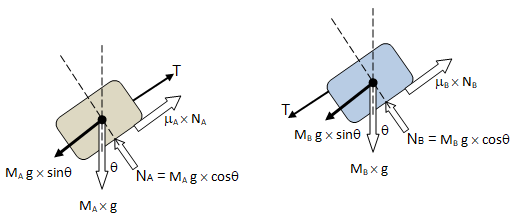
The acceleration can be calculated from force balance as explained below.
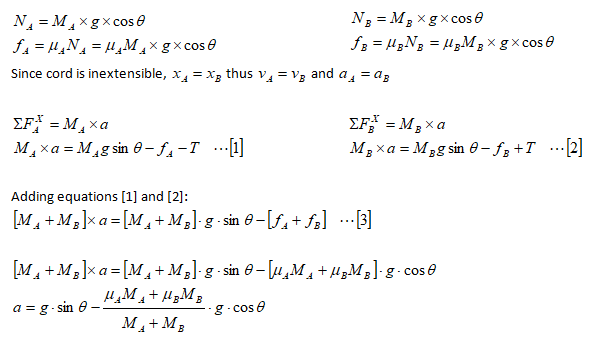
Tension in the cord can be calculated as follows.
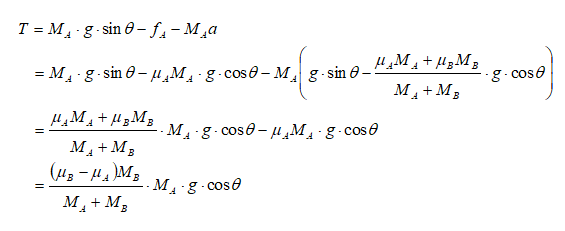
Relative Velocity, Conservation of Momentum
A gun whose barrel makes an angle 'θ' with the horizontal fires a bullet having muzzle velocity ‘U’ with respect to the barrel. The system is mounted on a frictional horizontal track with equal coefficients of static and dynamic coefficients. The mass of the gun-system is M and the mass of the bullet is m. Find the recoil velocity 'V' and the magnitude of the absolute velocity of the bullet as it leaves the gun.
Note that the problem changes state and there are two events in the system. Before bullet is fired and after bullet is fired. This is similar to situations encountered in problems dealing with collisions. Thus:
Momentum of the system (gun + bullet) before firing = 0Momentum of the system (gun + bullet) after firing = 0
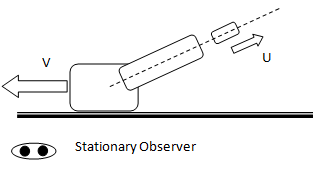
VGUN, GROUND = VGUN, BULLET + VBULLET, GROUND
VGUN, GROUND = -VBULLET, GUN + VBULLET, GROUND
-V = -(U * cosθ) + VBULLET, GROUND
VBULLET, GROUND = -V +(U * cosθ)
Total momentum of gun-system and bullet = 0. Thus:
[-V +(U * cosθ)] - MV = 0
V = m⁄M+m * U cosθ
Magnitude of absolute velocity of bullet:
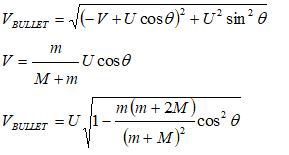
Relative Velocity, Conservation of Momentum
Two persons A and B of equal weight hold on to the two ends of a massless inextensible rope which passes over a frictionless massless pulley. 'A' starts climbing up the rope with a velocity VA,R relative to the rope, while B hangs on without climbing. Find the absolute velocity of B.
Since person 'B' just holds on the rope, his velocity relative to rope is zero. Hence, velocity of 'B' relative to ground = velocity of rope relative to ground. Note that the gravitation force acts on both A and B. Thus, if ground is not part of the system, the principle of conservation of momentum will not apply. However, if the Earth is included in the system, the gravitational pull becomes an internal force and cancel out.
Momentum of the system before 'A' starts climbing = 0
Momentum of the system after 'A' starts climbing = 0
VA,G = VA,R + VR,G
VA,G = VA,R + VB,G. Since VR,G = VB,G
Thus:
M * (VA,G + VB,G) = 0. That is: (VA,R + VB,G) + VB,G = 0.
Hence,|VB,G| = VA,R ⁄ 2
Rolling without Slipping
A cylinder of radius R is rolling without slipping on a horizontal surface. Find the relationship between the linear velocity V of the centre of the cylinder and the angular velocity ω of the cylinder.
The motion of the rolling cylinder can be described as shown below. Since, there is no slippage at the contact point between the cylinder and the horizontal surface, the linear travel (displacement) is equal to angular displcement.
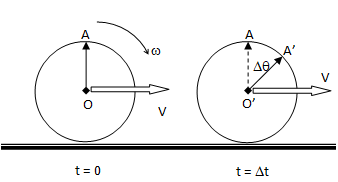
The linear displacement (OO’) is equal to arch length due to rotation (AA’). That is: V * Δt = R * Δθ. Thus:
Δθ⁄Δt = ω = V⁄R
Sliding without Rolling
A particle of mass m and radius r starts from rest and slides down the side of a hemispherical surface of radius R under the action of gravity. If there is no friction, and the particle starts from A, what force will be exerted on the surface by the particle at the instant when it is located at B? Assume R >> r.
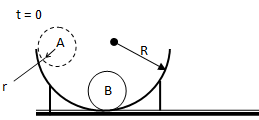
The free body diagram at some angular postion θ can be described as
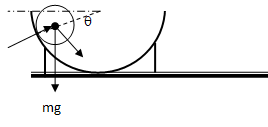
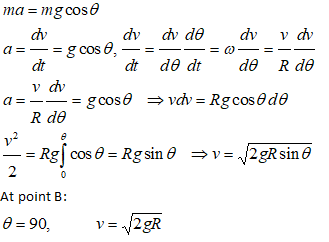
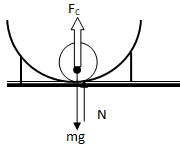
Centripetal force = FC = N – mg = mv2/R. Thus:
N = mg + m * 2gR/R = 3mg
Sliding without Toppling
What force should be applied to pull-out book B without toppling book C? Assume infinite frictional between book A and the table. Assume no moment on book C when book B is pulled-out completely.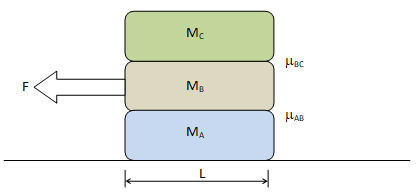
Note that to avoid toppling, the displacement of book C should be L/2 while the displacement of book B is L.
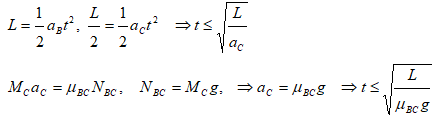
Thus, the required minimum acceleration of book B is:
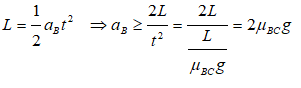
The free-body diagram of the two books are:
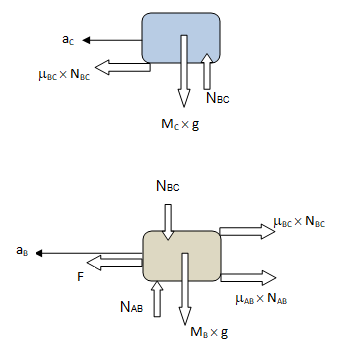
Important point to note in the FBD of book ‘B’ is the mass MB. Since, this is the FBD of book ‘B’, only its own mass will generate gravity force. The mass of book ‘A’ lying over it is manifested by reaction NBC.
Finally, the required minimum value of force F can be calculated from force balance as:
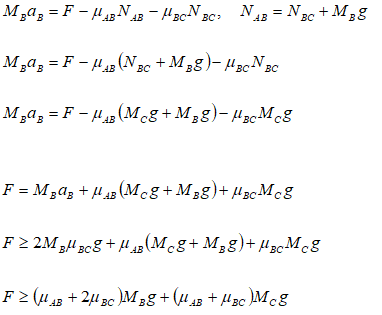
Sliding with Rolling
A solid spherical ball of mass M and radius R is initially thrown down a rough surface with an initial speed v0 and it starts sliding without rolling but due to friction it begins to roll. Using the torque method (Newton's second law for angular motion) about the center of mass, find the speed vROLL of the sphere when it just start to roll without slipping?The free-body diagram of the ball:
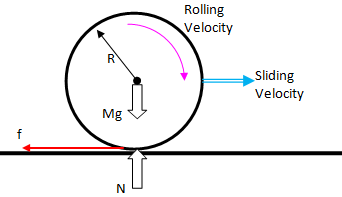
Important point to note:
- There is relative slippage between the ball and the ground, the friction will act opposite the linear motion of the centre of the ball.
- Gravity and normal reaction forces will exert no torque about the centre of the mass.
- As per the kinematics, the angular speed will increase as ω = ω0 + α * t. Since, ω0 = 0, ω = α * t.
- As per the kinematics, the linear speed will decrease as v = v0 + a * t, where a is decceleration (< 0) due to friction.
- At the instant ball stops sliding, the kinetic friction no longer acts, static friction at point of contact acts to prevent linear acceleration of the mass and the ball moves with constant angular and linear velocity. At this stage, v = ω * R.
Torque acting about centre of mass, τCG = ICG * α = R * f ... [I] where ICG is the mass moment of inertia about centre of mass (or centre of gravity) and α is the angular acceleration.
Applying Newton's second law for linear motion: m * a = -f, thus a = -f / m ... [II].Thus:
v(t) = v0 - f/m * t ... [III]
and
ω(t) = f * R / ICG * t ... [IV]
When ball starts rolling without slipping, vCG = ω * R. Thus, from equation [IV], vNO-SLIP = ωNO-SLIP * R = f * R2 / ICG * tROLL. Hence,
tROLL = time at which pure rolling starts = vNO-SLIP * ICG / f / R2.
Or,
tROLL * f = vNO-SLIP * ICG / R2.
From equation [III],
vNO-SLIP = v0 - f * tROLL / m = v0 - vNO-SLIP * ICG / R2 / m.
Finally, we get
vNO-SLIP = v0 / [1 + ICG / m / R2]. For hollow sphere, ICG = 2/3 * m * R2 and for solid shpere, ICG = 2/5 * m * R2.
Impulse Momentum Principle - Force due to Rain-drops
Chindren are playing in rain which is falling steadily at 10 [cm/hr]. The terminal velocity of rain drops can be assumed 5 [m/s] and the average radius of the head of the children to be 7.5 [cm]. What is the average force acting on the children's head dut to vertically falling rain drops.
Note that the rain intensity is specified in length per unit time such as 10 [cm/hr]. This means over unit m2, the water collected will have height of 10 [cm] in 1 [hr].
The mass flow rate of water in rain = 10 [cm/hr] * 1000 [kg/m3] * π * 7.52 [cm2] = 4.91 * 10-7 [kg/s].
Assuming all the water sticks with the head that is no splashing of the rain water in vertical direction, all the momentum is lost. Hence, force acting on the head = 4.91 * 10-7 [kg/s] * 5 [m/s] = 2.45 * 10-6 [N].Simple Harmonic Motion [SHM]
A frictionless piston of mass M is attached to a mass-less spring though a rod and disk arrangement of negligible mass. The pressure and temperature inside the gas chamber is p and T and the walls of the chamber have infinite thermal conductivity. The volume, cross-section area and diameter of the gas chamber are V, A and D respectively. Find the frequency of oscillation for small displacement of the piston.
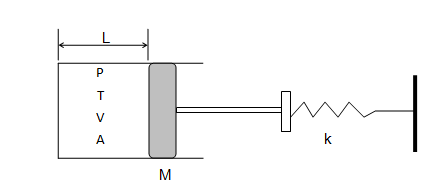
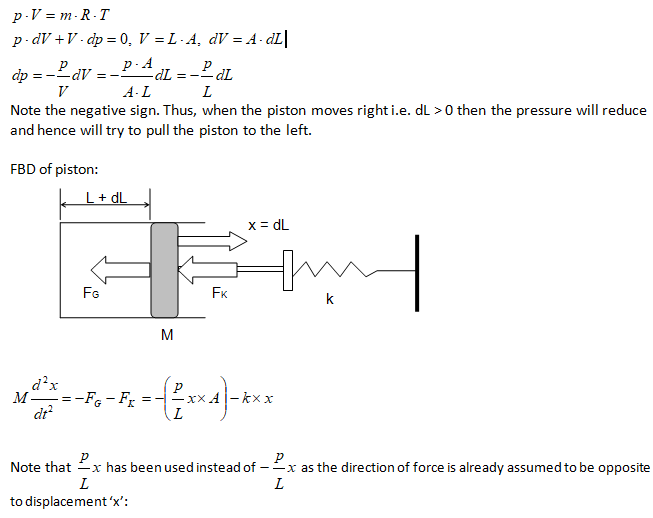
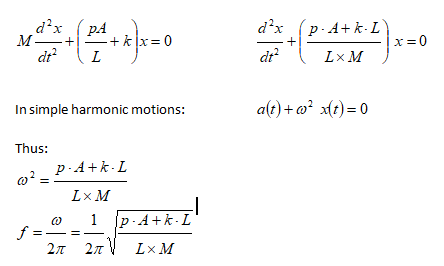
Step-1: Identify the mean (equilibrium) position. This is the static condition when any temporary force or support are not present and only forces continuourly acting in the system (gravity, buoyancy, hydrostatic pressure, spring force) are present. These forces are called "forces internal to the system".
Look for statement like "a mass is released from free length of spring, a ball is dropped from... All these cases might be a situation where SHM motion does not start from mean position.Step-2: Draw the Free-Body-Diagram [FBD] of mean position
Step-3: Assume a small displacement (disturbance) 'x' along the direction of force. Create new FBD under displacement condition
Step-4: Find the unbalanced (restoring) force and divide it by the (equivalent) mass of the system
Step-5: The coefficient of 'x' is the square of "angular frequency". Note that "angular frequency" and "angular velocity" both have same units but they have different meaning.
For example, a rod pinned at one end and rotating about it will have both angular velocity [rate of range of angle: dθ/dt] and the angular frequency [ω] - how fast is oscillates about its mean position.Standing and Traaveling Wave
The animation below give a visual difference between the two type of waves. It can also be found on YouTube.Pulley System
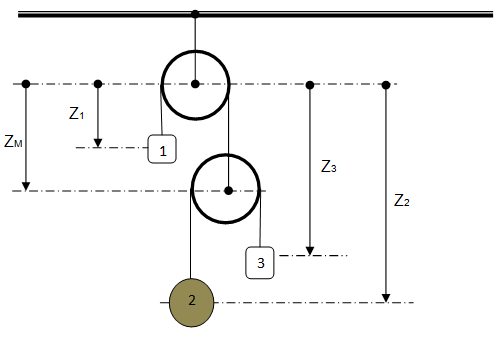
One of the fundamental rules to solve problems involving pulleys is to consider the “length of each independent cord” as constant.
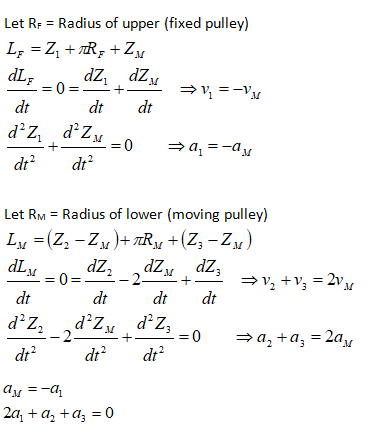
FBD of pulleys and masses are:
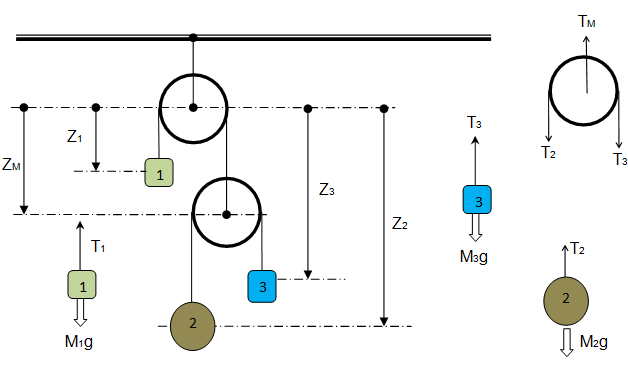
Newton's Second Law of Motion to masses and pulleys:
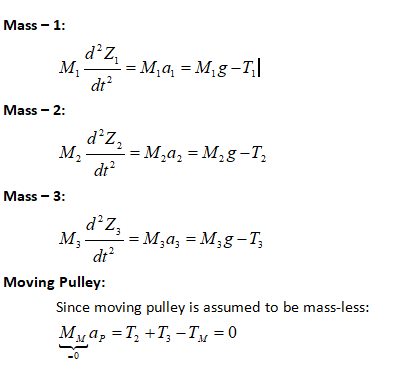
The next fundamental rule in situations dealing with pulleys is that the tension in a cord passing over any frictionless pulley remains constant in magnitude. Thus:
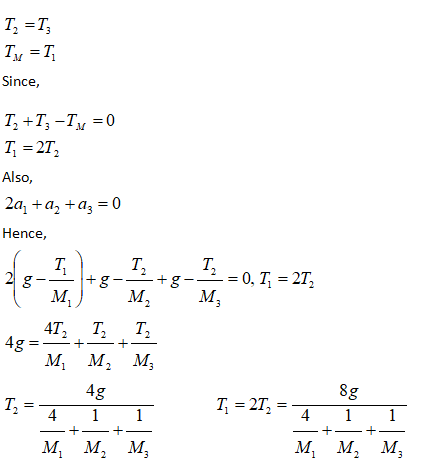
Flow in a Viscous (Resistive) Medium
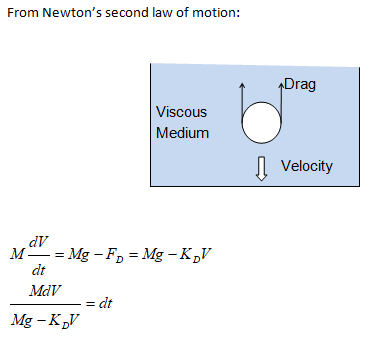
A body of mass M is falling through a viscous resisting medium subjected to a drag force proportional to the velocity squared that is FV = KD * V. If the body starts from rest, find expression for velocity at later times.

Impulse-Momentum Principle
A player hits the football which is moving away from him with velocity 0.5 [m/s] with 100.0 [N] of force. If the ball has a mass of 0.25 kg and is in contact with the strings of the racket for 0.025 seconds, what will be the velocity of the ball when it leaves the player’s foot?.
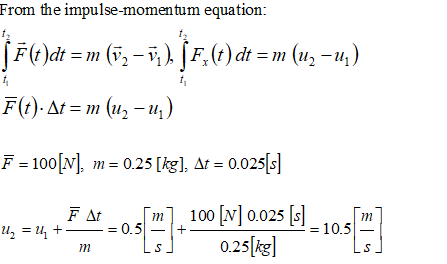
Pulling a cart up Inclined Plane
We know by experience that pulling a cart is easier than pushing - if frictional force is significant. Qualitatively this is because pull-action acts against gravity causing the normal reaction to reduce and hence the redcution in frictional force occurs.
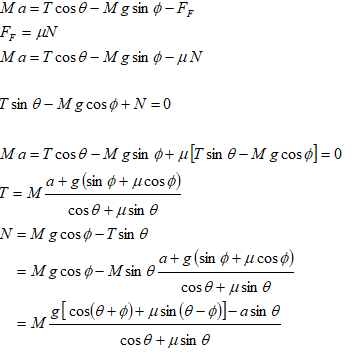
Pulling a rope up
A uniform solid rope of mass per unit length λ is coiled in a small pile on the floor. Its one end is tied with a massless inextensible cord which passes over a pulley. The other send of this cord is pulled down with a constant speed v. Find the force required when the rope has been raised to height x.
Let's assume that a time t, a length of rope x has been raised and a small segment of mass Δm is raised up in time Δt. Hence, impulse = f(t) * Δt. The change in momentum = Δm * v.
From Impulse-Momentum equation: f(t) * Δt = Δm * v, that is f(t) = v * Δm / Δt = v * (λ * v)
Weight of rope of length x, W = λ * x * g. Hence, total force require to be applied = F(t) = f(t) + λ * x * g = λ * [v2 + x * g].
Falling of a rope
A uniform solid rope of mass per unit length λ is free falling on the floor. Assume that the rope hits the same location. Find the force acting on the floor when a length x has already fallen over.
This problem is opposite to the previous problem. Additionally, the rope is falling with an acceleration 'g' and not at constant velocity.Let's assume that a time t when a length of rope x has already fallen, a small segment of mass Δm fall in time Δt. Hence, impulse = f(t) * Δt. The change in momentum = Δm * v.
From Impulse-Momentum equation: f(t) * Δt = Δm * v, that is f(t) = v * Δm / Δt = v * (λ * v).
From equation v2=u2 + 2gs, v2 = 2gx
Weight of rope of length x, W = λ * x * g. Hence, total force require to be applied = F(t) = f(t) + λ * x * gThus, F(t) = λ * [v2 + x * g] = 3λ * x * g.
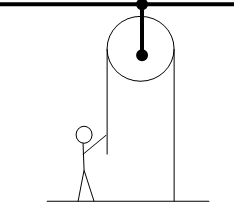
Pulling oneself upward
A person of mass M stands on a platform of mass m and pulls himself up by a rope that runs over a mass-less pulley. He pulls the rope with a force of magnitude F. Find the acceleration of platform.
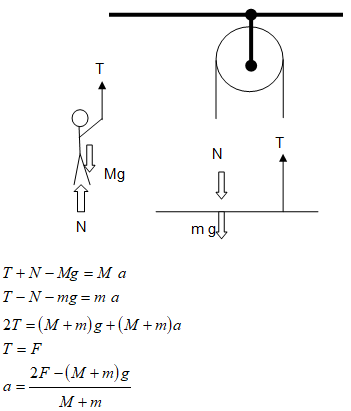
Work Energy Method
A person of mass 'm' is suspended from a roof on a cord of negligible mass having a length L. Assuming cord is behaving as a spring with spring constant k, and that L is the stretched length, calculate the work which the person would have to do to climb to the roof. Compare this with the work required to climb when cord is inextensible. Treat person as a point mass.
Extension of the cord: x = m * g / k
Potential energy of the system when person is at the floor:
Potential energy of spring + potential energy of the person, VA = 1/2 * k * x2 + 0 = (1/2k) * m2 * g2.Potential energy of the system when person is at the roof:
Potential energy of spring + potential energy of the person, VB = 0 + m * g * L = m * g * L.Work done by the person, W1 = - Work done by the (gravity + spring) forces = VB - VB
W1 = m * g / (2k) * [2 * k * L - m * g]
Work done when the cord is inextensible, W2 = m * g * LRelative Sliding of Blocks with Friction
Two blocks of mass MA and MB are in contact as shown. The coefficient of kinetic friction between all surfaces is μk. Find the magnitude of the horizontal force F necessary to drag block B to the left at a constant speed if A and B are connected by a massless flexible but inextensible thread passing around a fixed, frictionless pulley
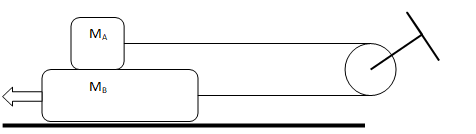
Since there is no acceleration, the problem gets highly simplified if the system can be visualized as shown below. Note that this is applicable only when the blocks are moving at constant velocity. This is not applicable if block B and A are accelerating in opposite direction.
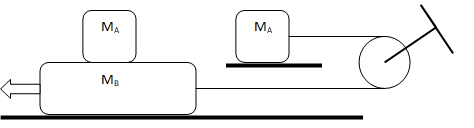
Relative Sliding of Blocks without Friction
Two blocks of mass M and m are in contact as shown. The coefficient of kinetic friction between all surfaces is 0. Find the magnitude of the horizontal velocity V of the block M when mass m just reached the ground level.

Oblique Collision
An oblique collision is said to occur when the line of impact is not parallel to direction of velocities of colliding bodies.- The conservation of angular momentum applies to both along and perpenducalr to the line of imptact.
- If the balls are smooth, there is no force acting between them at right angles to the line of impact.
v.sinβ = u.sinφ, v.cosβ = e × (u. cosφ)
Finally: cotβ = e.cotφ
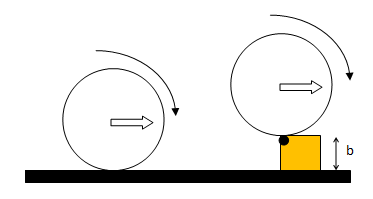
Climbing a curb
The minimum velocity required to climb a curb of height 'b' by a hollow spherical ball of radius R and mass m can be calculated using conservation of angular momentum and conservation of energy.
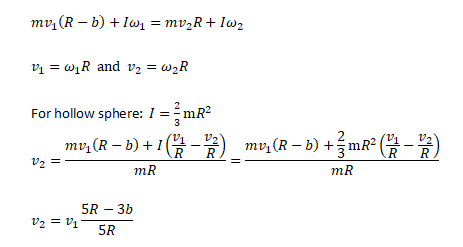
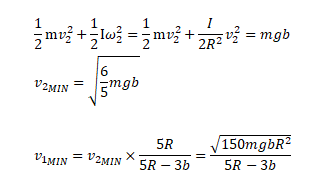
Newton's Law of Cooling
The rate of cooling of a block considered as lumped mass is directly proportional to the difference of instantaneous temperature and the temperature of the surroundings.

Gravitational Potential
A particle is dropped with zero initial velocity at the surface of the earth through a hole drilled diametrically in the earth. What would be the velocity of the particle when it reachs the center of the earth?
In a conservative force field, change in the potential energy = negative of the work done by the force. Potential at the suface of the earth (centre of any solid sphere of mass M), V1 = -GM/R, where G = Universal Constant of Gravitation, M = Mass of the earth and R is the radius.
Potential at the centre of the earth, V2 = -3GM/2R.From conservation of total energy, (P.E. + K.E.)SURFACE = (P.E. + K.E.)CENTRE, the change in kinetic energy = 1/2 * m * v2 = m * [-GM/R - (-3GM/2R)] = GMm/2R. Also, acceleration due to gravity, 'g' = GM/R2.
Thus: 1/2 * m * v2 = m * g * R/2. Hence, v = [gR]0.5.Another approach to solve this question would be to apply Newton's law of motion where the force acting on the particle varies as F(r) = GM(r)m/r2. Here, r = instantaneous radius of the particle, M(r) = Mass of earth of radius r = M * r3 / R3.
dW = F.dr = GM/R3.rdr.
Also, work done upon the mass m by the force F is equal to the change in the kinetic energy of the mass. Hence,
ΔKE = GM/2R = 1/2 * m * v2.
Potential Energy - Liquid Column
Two vertical cylindrical tanks of area A1 and A2 are inter-connected. Initally water level in each tank is H above the horizontal pipe connecting the two. The fluid in tank '1' is pushed down by a distance x. Find the potential energy of the system as a function of x, the density of the fluid ρ, and the areas of the tanks. Neglect frictional losses while the liquid level was depressed. 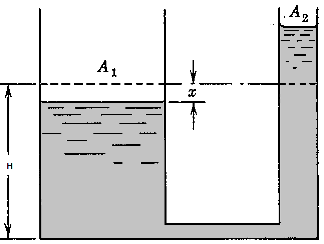
From conservation of mass: A1 * ρ * x = A2 * ρ * x2. Thus: x2 = A1/A2 * x.
[Incorrect Method]: As per change in centre of mass of the displaced volume of the liquid in two tanks:
Change (reduction) in P.E. of tank 1: ΔPE1 = - [A1 * x * ρ] * g * x/2.Change (increase) in P.E. of tank 2: ΔPE2 = [A1 * ρ * x] * g * [A1/A2 * x/2].
ΔPE = ΔPE1 + ΔPE2 = A1 * ρ * g * x2/2 [A1/A2 - 1].
[Correct Method]: Change in potential energy = Negative of work done by force acting on left column
F(x) = p(x) * A1, p(x) = ρ * g * [x + x2] = ρ * g * x [1 + A1/A2].
Since, force and displacements are in opposite directions: dW = -F(x)* dx
W = - A1 * ρ * g * x2/2 [1 + A1/A2].Thus, ΔPE = -W = A1 * ρ * g * x2/2 [1 + A1/A2].
Bead Sliding on a Rod Rotating in Horizontal Plane about it mid-point:


The content on CFDyna.com is being constantly refined and improvised with on-the-job experience, testing, and training. Examples might be simplified to improve insight into the physics and basic understanding. Linked pages, articles, references, and examples are constantly reviewed to reduce errors, but we cannot warrant full correctness of all content.
Copyright © 2017 - All Rights Reserved - CFDyna.com
Template by OS Templates